
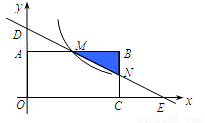
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数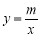 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(1)过O,B,E三点的二次函数关系式为:y=﹣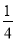 x2+
x2+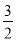 x;
x;
(2)直线DE的解析式为:y=﹣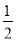 x+3;M(2,2);
x+3;M(2,2);
(3)点N在函数y=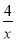 的图象上.
的图象上.
【解析】
试题分析:(1)首先把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,得方程,解此方程即可;
(2)首先设直线DE的解析式为:y=kx+b,然后将点D,E的坐标代入即可求得直线DE的解析式,又由点M在AB边上,B(4,2),而四边形OABC是矩形,可得点M的纵坐标为2,求得点M的坐标;
(3)由反比例函数y= (x>0)的图象经过点M,可求该反比例函数的解析式,又由点N在BC边上,B(4,2),可得点N的横坐标为4.然后由点N在直线y=﹣
(x>0)的图象经过点M,可求该反比例函数的解析式,又由点N在BC边上,B(4,2),可得点N的横坐标为4.然后由点N在直线y=﹣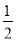 x+3上,求得点N的坐标,即可判断.
x+3上,求得点N的坐标,即可判断.
试题解析:(1)设过O,B,E三点的二次函数关系式为:y=ax2+bx+c;
把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,得 ,
,
解得: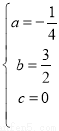 ,
,
∴过O,B,E三点的二次函数关系式为:y=﹣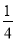 x2+
x2+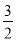 x;
x;
(2)设直线DE的解析式为:y=kx+b,
∵点D,E的坐标为(0,3)、(6,0),
∴ ,
,
解得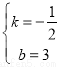 ,
,
∴直线DE的解析式为:y=﹣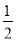 x+3;
x+3;
∵点M在AB边上,B(4,2),而四边形OABC是矩形,
∴点M的纵坐标为2.
又∵点M在直线y=﹣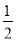 x+3上,
x+3上,
∴2=﹣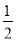 x+3.
x+3.
∴x=2.
∴M(2,2);
(3)∵y= (x>0)经过点M(2,2),
(x>0)经过点M(2,2),
∴m=4.
∴该反比例函数的解析式为:y=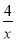 ,
,
又∵点N在BC边上,B(4,2),
∴点N的横坐标为4.
∵点N在直线y=﹣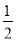 x+3上,
x+3上,
∴y=1.
∴N(4,1).
∵当x=4时,y=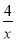 =1,
=1,
∴点N在函数y=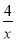 的图象上.
的图象上.
考点:反比例函数综合题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,AC=10,将BC向BA方向翻折过去,使点C落在BA上的点C′,折痕为BE,则EC的长度是 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:选择题
如图,等腰梯形ABCD中,AD∥BC,AB=5,BC=8,∠BAD的平分线交BD于点E,且AE∥CD,则梯形ABCD的周长为( )

A.21 B.18 C.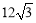 D.10
D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:选择题
如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则 ∠B的度数为( )
A.30° B.34° C.38° D.68°

查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:填空题
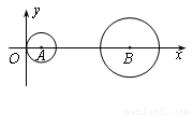
如图,已知点A(1,0)、B(7,0),⊙A、⊙B的半径分别为1和2,当⊙A与⊙B相切时,应将⊙A沿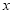 轴向右平移__________个单位.
轴向右平移__________个单位.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,设点P到原点O的距离为 ,OP与x轴正方向的夹角为
,OP与x轴正方向的夹角为 ,则用[
,则用[ ,
, ]表示点P的极坐标;显然,点P的极坐标与它的坐标存在一一对应的关系.例如,点P的坐标(1,1),则极坐标为[
]表示点P的极坐标;显然,点P的极坐标与它的坐标存在一一对应的关系.例如,点P的坐标(1,1),则极坐标为[ ,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
A. B.
B. C.
C. D.(2,2)
D.(2,2)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:解答题
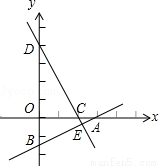
已知:如图一次函数y=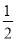 x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com