练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

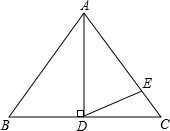
    如图，△ABC为等边三角形，AD为BC边上的高，E为AC边上的一点，且AE=AD，则∠EDC=__________．


    15°．

    【考点】等边三角形的性质．

    【分析】先根据等边三角形的性质得出∠BAC=60°，再由AD⊥BC得出∠CAD的度数，根据AE=AD求出∠ADE的度数，由∠EDC=∠ADC﹣∠ADE即可得出结论．

    【解答】解：∵△ABC是等边三角形，

    ∴∠BAC=60°．

    ∵AD⊥BC，

    ∴∠CAD=30°，∠ADC=90°，

    ∵AE=AD，

    ∴∠ADE==75°，

    ∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°．

    故答案为：15°．

    【点评】本题考查的是等边三角形的性质，熟知等边三角形三线合一的性质是解答此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列各式中，从左到右的变形是因式分解的是              （    ）.

    A.           B.   

    C.  a2－4ab+4b2=(a－2b)2             D.  ax+ay+a=a(x+y)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若（a+1）2+|b﹣3|=0，则ab=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，∠CBD、∠ADE为△ABD的两个外角，∠CBD=70°，∠ADE=149°，则∠A的度数是(     )

    A．28°   B．31°    C．39°   D．42°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知在△ABC中，PR⊥AB于R，PS⊥AC于S，PR=PS，∠1=∠2，则四个结论：①AR=AS；②PQ∥AB；③△BPR≌△CPS；④BP=CP中(     )

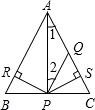
    A．全部正确 B．仅①②正确     C．仅①正确 D．仅①④正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将一张矩形纸条ABCD按如图所示折叠，若折叠角∠FEC=64°．

    （1）求∠1的度数；

    （2）求证：△EFG是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列说法中正确的个数是(     )

    （1）﹣a表示负数；           

    （2）多项式﹣3a2b+7a2b2﹣2ab+l的次数是3；

    （3）单项式﹣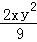的系数为﹣2；

    （4）若|x|=﹣x，则x＜0．

    A．0个  B．1个   C．2个  D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


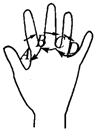
    如图，在各个手指间标记字母A，B，C，D．请按图中箭头所指方向（即A→B→C→D→C→B→A→B→C→…的方式）从A开始数连续的正整数1，2，3，4，…．当字母C第2015次出现时，数到的数恰好是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    单项式﹣的系数是(     )

    A．    B．﹣ C．      D．﹣

    查看答案和解析>>

    同步练习册答案