
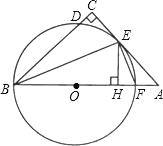
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF;(3)由(2)中CD=HF,即可求出HF的值,先求OA和OF的长度,再由AF=OA-OF求出AF的值;
试题解析:
(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;
(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF
证明:(1)如图,连接OE.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)如图,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
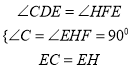 ,
,
∴△CDE≌△HFE(AAS),
∴CD=HF.
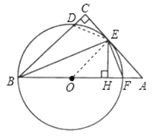
(3)由(2)得,CD=HF.又CD=1
∴HF=1
在Rt△HFE中,EF=![]() =
=![]()
∵EF⊥BE
∴∠BEF=90°
∴∠EHF=∠BEF=90°
∵∠EFH=∠BFE
∴△EHF∽△BEF
∴![]() ,即
,即![]()
∴BF=10
∴![]() ,
, ![]() ,
,
∴在Rt△OHE中, ![]() ,
,
∴在Rt△EOA中, ![]() ,
,
∴![]()
∴![]()
∴![]() .
.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: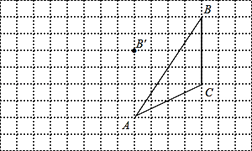
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线nx+(n+1)y= ![]() (n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
(n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC
(1)如图1,若α+β= ![]() ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(﹣2,3)向右平移a个单位长度,再向下平移b个单位长度,平移后对应的点为A′,且点A和A′关于原点对称,则a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1,0),且﹣2<x1<1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣![]() ;⑤2a<b+
;⑤2a<b+![]() ,正确的是( )
,正确的是( )
A. ①③ B. ①②③ C. ①②③⑤ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com