【题目】下列说法中，不正确的是（ ）
A. 直角边长分别是6、4和4.5、3的两个直角三角形相似 B. 底角为40°的两个等腰三角形相似
C. 一个锐角为30°的两个直角三角形相似 D. 有个角为30°的两个等腰三角形相似
科目：初中数学 来源： 题型：
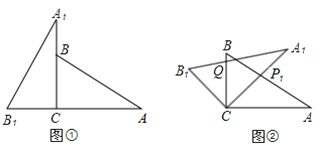
【题目】将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．
（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；
（2）在图②中，若AP1=2，则CQ等于多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
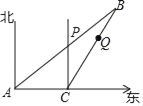
【题目】如图所示，甲、乙两船同时由港口A出发开往海岛B，甲船沿某一方向直航140海里的海岛B，其速度为14海里/小时；乙船速度为20海里/小时，先沿正东方向航行3小时后，到达C港口接旅客，停留1小时后再转向北偏东30°方向开往B岛，其速度仍为20海里/小时．
（1）求海岛B到航线AC的距离；
（2）甲船在航行至P处，发现乙船在其正东方向的Q处，问此时两船相距多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在△ABC中，∠ACB=90°，BC=2，AC=4，点D在射线BC上，以点D为圆心，BD为半径画弧交边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC于点G．
（1）求证：△EFG∽△AEG；
（2）设FG=x，△EFG的面积为y，求y关于x的函数解析式并写出定义域；
（3）联结DF，当△EFD是等腰三角形时，请直接写出FG的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
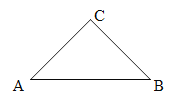
【题目】如图，在△ABC中，∠ACB=90°，AC=BC=4．
(1)尺规作图：将△ABC绕AC的中点O为旋转180°，点B的对应点为B′（保留作图痕迹，不写做法）；
(2)求点B与点B′之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】身高相等的四名同学甲、乙、丙、丁参加风筝比赛，四人放出风筝的线长、线与地面的夹角如下表（假设风筝线是拉直的），则四名同学所放的风筝中最高的是（ ）
同学 | 甲 | 乙 | 丙 | 丁 |
放出风筝线长 | 140m | 100m | 95m | 90m |
线与地面夹角 | 30° | 45° | 45° | 60° |
A、甲B、乙
C、丙D、丁
查看答案和解析>>
科目：初中数学 来源： 题型：
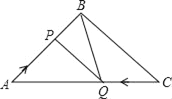
【题目】如图，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿着CA以每秒3cm的速度向A点运动，设运动时间为x秒．
（1）x为何值时，PQ∥BC；
（2）是否存在某一时刻，使△APQ∽△CQB？若存在，求出此时AP的长；若不存在，请说明理由；
（3）当
＝
时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
.
(1)求该二次函数图象与x轴的交点坐标；
(2)若m＜0，当1≤x≤4时，y的最大值是2，求当1≤x≤4时，y的最小值；
(3)已知P（2，
），Q（4，）为平面直角坐标系中两点，当抛物线与线段PQ有公共点时，请求出m的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
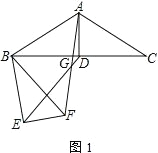
【题目】(1) 如图，AD 是等腰△ABC 的中线，AB＝AC．把△BDA 绕 B 点顺时针旋转α角度（0°＜α＜90°）得到△BEF，点 D 对应 E 点，点 A 对应 F 点，AF 与 DE 交于点 G。
① 求证：△BAF∽△BDE
② 求证：AG＝FG
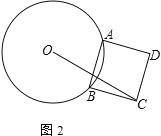
(2) 如图，AB 是⊙O 的一条运动的弦，以 AB 为边向圆外作正方形 ABCD．若⊙O 的半径为 2， 则 OC 的长的最大值是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
