
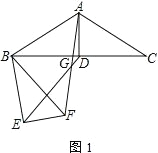
【题目】(1) 如图,AD 是等腰△ABC 的中线,AB=AC.把△BDA 绕 B 点顺时针旋转α角度(0°<α<90°)得到△BEF,点 D 对应 E 点,点 A 对应 F 点,AF 与 DE 交于点 G。
① 求证:△BAF∽△BDE
② 求证:AG=FG
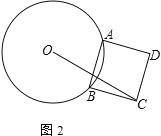
(2) 如图,AB 是⊙O 的一条运动的弦,以 AB 为边向圆外作正方形 ABCD.若⊙O 的半径为 2, 则 OC 的长的最大值是
【答案】(1) 见详解;(2)![]() .
.
【解析】
(1) ①根据旋转的性质,得到∠ABD=∠FBE,![]() , AB=FB,∠ABF=∠DBE,可得证;
, AB=FB,∠ABF=∠DBE,可得证;
②证明△BHE∽△GHF,△BHG∽△EHF,得到∠BGF=90°,由 (1) 中AB=BF,得证AG=FG;
(2) 根据勾股定理得到OC=OB+BC,可知当当AB为圆的直径时,OC有最大值.
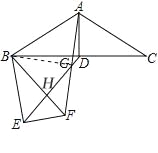
(1) ①∵△ABD旋转到△FBE, ∴∠ABD=∠FBE,![]() , AB=FB,
, AB=FB,
∴∠ABD+∠DBF=∠FBE+∠DBF,即∠ABF=∠DBE,
∴△BAF∽△BDE;
②联结BG,令BF、EG交于H,
∵△BAF∽△BDE,
∴∠AFB=∠DEB,
又∵∠BHE=∠GHF,
∴△BHE∽△GHF,
∴![]() ,
,
又∵∠BHG=∠EHF,
∴△BHG∽△EHF,
∴∠GBH=∠FEH,
∵∠BEH+∠FEH=∠GFH+∠GBH=90°,
∴∠BGF=90°, 即BG⊥AF,
又∵AB=BF,
∴AG=GF;
(2) 由勾股定理得OC=OB+BC,
∵半径OB=2,
∴当BC为最大时,OC有最大值,
又∵在正方形 ABCD中,AB=BC,
∴当AB为圆的直径时,OC有最大值=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A. 直角边长分别是6、4和4.5、3的两个直角三角形相似 B. 底角为40°的两个等腰三角形相似
C. 一个锐角为30°的两个直角三角形相似 D. 有个角为30°的两个等腰三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新课程改革十分关注学生的社会实践活动,小明在一次社会实践活动中负责了解他所居住的小区500户居民的家庭月人均收入情况,他从中随机调查了40户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 | 频数 | 占比 |
1000≤x<2000 | 3 | 7.5% |
2000≤x<3000 | 5 | 12.5% |
3000≤x<4000 | a | 30% |
4000≤x<5000 | 8 | 20% |
5000≤x<6000 | b | c |
6000≤x<7000 | 4 | 10% |
合计 | 40 | 100% |
(1)频数分布表中,a= ,b= ,C= ,请根据题中已有信息补全频数分布直方图;
(2)观察已绘制的频数分布直方图,可以看出组距是 ,这个组距选择得 (填“好”或“不好”),并请说明理由.
(3)如果家庭人均月收入“大于3000元不足6000元”的为中等收入家庭,则用样本估计总体中的中等收入家庭大约有 户.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的调控下,某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7两月平均每月降价的百分率;
(2)如果房价继续回落,按此降价的百分率,请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
【1】在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
【1】如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=![]() ,求BC的长.
,求BC的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com