
【题目】如图,△ABC内接于⊙O,DA、DC分别切⊙O于A、C两点,∠ABC=114°,则∠ADC的度数为_______°.

科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
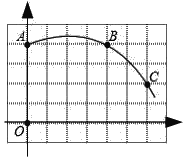
【题目】如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;.
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线交
的直线交![]() 轴负半轴于
轴负半轴于![]() ,且
,且![]() .
.

(1)求直线![]() 的函数表达式:
的函数表达式:
(2)如图2, ![]() 为
为![]() 轴上
轴上![]() 点右侧的一动点,以
点右侧的一动点,以![]() 为直角顶点,
为直角顶点,![]() 为一腰在第一象限内作等腰直角三角形
为一腰在第一象限内作等腰直角三角形![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() .当
.当![]() 点运动时,
点运动时,![]() 点的位置是否发生变化?如果不变请求出它的坐标:如果变化,请说明理由.
点的位置是否发生变化?如果不变请求出它的坐标:如果变化,请说明理由.
(3)直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,是否存在这样的直线
,是否存在这样的直线![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,点
,点![]() 在
在![]() 轴的负半轴上,若将
轴的负半轴上,若将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴正半轴上的点
轴正半轴上的点![]() 处.
处.
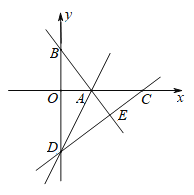
(1)求![]() 的长;
的长;
(2)求点![]() 和点
和点![]() 的坐标;
的坐标;
(3) ![]() 轴上是否存在一点
轴上是否存在一点![]() , 使得
, 使得![]() ?若存在,直接写出点
?若存在,直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
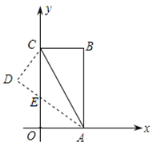
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() ,
,![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴上,连接
轴上,连接![]() ,将纸片
,将纸片![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 的位置,
的位置,![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
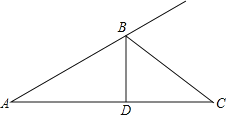
【题目】如图,在△ABC中,BD⊥AC,垂足为C,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.
(1)请同学们根据以上提示,在上图基础上补全示意图.
(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生的十次数学竞赛训练成绩的平均分分别是![]() 和
和![]() ,成绩的方差分别是
,成绩的方差分别是![]() 和
和![]() ,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
A. 甲、乙两人平均分相当,选谁都可以
B. 乙的平均分比甲高,选乙
C. 乙的平均分和方差都比甲高,成绩比甲稳定,选乙
D. 两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com