
【题目】在国家政策的调控下,某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7两月平均每月降价的百分率;
(2)如果房价继续回落,按此降价的百分率,请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元?请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求该二次函数图象与x轴的交点坐标;
(2)若m<0,当1≤x≤4时,y的最大值是2,求当1≤x≤4时,y的最小值;
(3)已知P(2,![]() ),Q(4,
),Q(4,![]() )为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
)为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )

A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
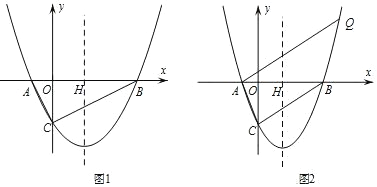
【题目】已知,抛物线 y=![]() x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=
x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=![]() 交 x 轴于点 H.
交 x 轴于点 H.
(1)若抛物线y=![]() x2+bx+c经过点(﹣4,6),求抛物线的解析式;
x2+bx+c经过点(﹣4,6),求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
(3)如图 2,过点A作AQ∥BC交抛物线于点Q,若点Q的纵坐标为﹣![]() c, 求点Q的坐标.
c, 求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
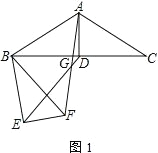
【题目】(1) 如图,AD 是等腰△ABC 的中线,AB=AC.把△BDA 绕 B 点顺时针旋转α角度(0°<α<90°)得到△BEF,点 D 对应 E 点,点 A 对应 F 点,AF 与 DE 交于点 G。
① 求证:△BAF∽△BDE
② 求证:AG=FG
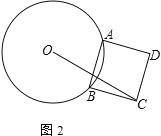
(2) 如图,AB 是⊙O 的一条运动的弦,以 AB 为边向圆外作正方形 ABCD.若⊙O 的半径为 2, 则 OC 的长的最大值是
查看答案和解析>>
科目:初中数学 来源: 题型:
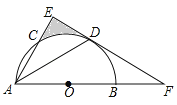
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 在抛物线
在抛物线![]() (
(![]() )上,且
)上,且![]() ,
,
(1)若![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)若该抛物线与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() ,试求出
,试求出![]() ,
,![]() 的数量关系;
的数量关系;
(3)将该抛物线平移,平移后的抛物线仍经过![]() ,点
,点![]() 的对应点
的对应点![]() ,当
,当![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com