
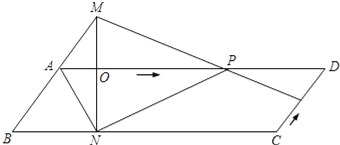
【题目】已知:如图,ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1).
(1)当t为何值时,四边形AQDM是平行四边形?
(2)证明:在P、Q运动的过程中,总有CQ=AM;
(3)是否存在某一时刻t,使四边形ANPM的面积是平行四边形ABCD的面积的一半?若存在,求出相应的t值;若不存在,说明理由.
【答案】(1) 是 (2)见解析 (3) 当t=![]() s时,四边形ANPM的面积是平行四边形ABCD的面积的一半
s时,四边形ANPM的面积是平行四边形ABCD的面积的一半
【解析】试题分析: (1)连结AQ、MD,根据平行四边形的对角线互相平分得出AP=DP,代入求出即可;
(2)根据已知得出△AMP∽△DQP,再根据相似三角形的性质得出![]() =
=![]() ,求出AM的值,从而得出在P、Q运动的过程中,总有CQ=AM;
,求出AM的值,从而得出在P、Q运动的过程中,总有CQ=AM;
(3)根据已知条件得出BN=MN,再根据BM=AB+AM,由勾股定理得出BN=MN=![]() (1+t),根据四边形ABCD是平行四边形,得出MN⊥AD,设四边形ANPM的面积为y,得出y=
(1+t),根据四边形ABCD是平行四边形,得出MN⊥AD,设四边形ANPM的面积为y,得出y=![]() ×AP×MN,假设存在某一时刻t,四边形ANPM的面积是平行四边形ABCD的面积的一半,得出
×AP×MN,假设存在某一时刻t,四边形ANPM的面积是平行四边形ABCD的面积的一半,得出![]() t2+
t2+![]() t=
t=![]() ×3×
×3×![]() ,最后进行整理,即可求出t的值.
,最后进行整理,即可求出t的值.
试题解析:
(1)连结AQ、MD,
∵当AP=PD时,四边形AQDM是平行四边形,
∴3t=3﹣3t,
解得:t=![]() ,
,
∴t=![]() s时,四边形AQDM是平行四边形.
s时,四边形AQDM是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△AMP∽△DQP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AM=t,
即在P、Q运动的过程中,总有CQ=AM;
(3)∵MN⊥BC,
∴∠MNB=90°,
∵∠B=45°,
∴∠BMN=45°=∠B,
∴BN=MN,
∵BM=AB+AM=1+t,
在Rt△BMN中,由勾股定理得:BN=MN=![]() (1+t),
(1+t),
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵MN⊥BC,
∴MN⊥AD,
设四边形ANPM的面积为y,
∴y=![]() ×AP×MN=
×AP×MN=![]() ×3t×
×3t×![]() (1+t)=
(1+t)=![]() t2+
t2+![]() t(0<t<1).
t(0<t<1).
假设存在某一时刻t,四边形ANPM的面积是平行四边形ABCD的面积的一半,
∴![]() t2+
t2+![]() t=
t=![]() ×3×
×3×![]() ,
,
整理得:t2+t﹣1=0,
解得:t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴当t=![]() s时,四边形ANPM的面积是平行四边形ABCD的面积的一半.
s时,四边形ANPM的面积是平行四边形ABCD的面积的一半.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4的图象经过点(﹣3,﹣2).
(1)求这个函数表达式;
(2)画出该函数的图象.
(3)判断点(3,5)是否在此函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
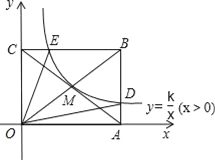
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com