
【题目】在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“相等点”,例如点![]() ,
,![]()
![]() 都是“相等点”,显然“相等点”有无数个.
都是“相等点”,显然“相等点”有无数个.
(1)若点![]() 是反比例函数
是反比例函数![]() 为常数,
为常数,![]() )的图象上的“相等点”,求这个反比例函数的解析式;
)的图象上的“相等点”,求这个反比例函数的解析式;
(2)一次函数![]() 为常数,
为常数,![]() )的图象上存在“相等点”吗?若存在,请用含
)的图象上存在“相等点”吗?若存在,请用含![]() 的式子表示出“相等点”的坐标,若不存在,说明理由;
的式子表示出“相等点”的坐标,若不存在,说明理由;
(3)若二次函数![]() 为常数)的图象上有且只有一个“相等点”,令
为常数)的图象上有且只有一个“相等点”,令![]() 当
当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时不存在,当
时不存在,当![]() 时存在.理由见解析;当
时存在.理由见解析;当![]() 时,函数
时,函数![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)根据相等点的定义求得![]() 的值,再用待定系数法求得解析式;
的值,再用待定系数法求得解析式;
(2)设![]() 是一次函数
是一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,代入解析式求得
的图象上的“相等点”,代入解析式求得![]() 便可;
便可;
(3)若二次函数![]() ,
,![]() 为常数)的图象上有且只有一个“相等点”,则二次函数
为常数)的图象上有且只有一个“相等点”,则二次函数![]() 与直线
与直线![]() 有且只有一个交点,由此得一元二次方程
有且只有一个交点,由此得一元二次方程![]() 的有且只有2个相等的实数根,由此列出
的有且只有2个相等的实数根,由此列出![]() 和
和![]() 的关系式,进而根据
的关系式,进而根据![]() 的取值范围求得
的取值范围求得![]() 的取值范围,再求
的取值范围,再求![]() 的取值范围便可.
的取值范围便可.
解:(1)![]() 点
点![]() 是反比例函数
是反比例函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,
的图象上的“相等点”,
![]() ,
,
![]() ,
,
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() 反比例的解析式为
反比例的解析式为![]() ;
;
(2)![]() 设
设![]() 是一次函数
是一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,则
的图象上的“相等点”,则
![]() ,
,
![]() ,
,
当![]() ,即
,即![]() 时,方程无解,则此时一次函数
时,方程无解,则此时一次函数![]() 为常数,
为常数,![]() 的图象上不存在“相等点”,
的图象上不存在“相等点”,
当![]() ,即
,即![]() 时,得
时,得![]() ,则此时一次函数
,则此时一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ,
,![]() ,
,
故当![]() 时,一次函数
时,一次函数![]() 为常数,
为常数,![]() 的图象上不存在“相等点”;当
的图象上不存在“相等点”;当![]() 时,一次函数
时,一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ,
,![]() .
.
(3)![]() 二次函数
二次函数![]() ,
,![]() 为常数)的图象上有且只有一个“相等点”,
为常数)的图象上有且只有一个“相等点”,
![]()
![]() 只有一个解,
只有一个解,
![]() ,即
,即![]() 有两个相等的实数根,
有两个相等的实数根,
![]() △
△![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.
(1)求A,B两种商品每件的进价分别是多少元?
(2)为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
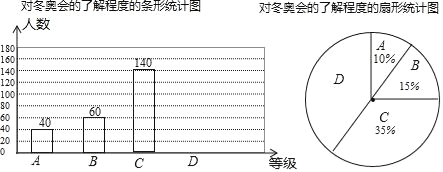
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一驴友分三次从![]() 地出发沿着不同线路(
地出发沿着不同线路(![]() 线、
线、![]() 线、
线、![]() 线)去
线)去![]() 地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;
地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;![]() 线、
线、![]() 线路程相等,都比
线路程相等,都比![]() 线路程多
线路程多![]() ;
;![]() 线总时间等于
线总时间等于![]() 线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完
线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完![]() 线;在
线;在![]() 线中穿越丛林、涉水行走和攀登所用时间分别比
线中穿越丛林、涉水行走和攀登所用时间分别比![]() 线上升了
线上升了![]() .若他用了
.若他用了![]() 小时穿越丛林、
小时穿越丛林、![]() 小时涉水行走和
小时涉水行走和![]() 小时攀登走完
小时攀登走完![]() 线,且
线,且![]() 都为正整数,则
都为正整数,则![]() _____.
_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
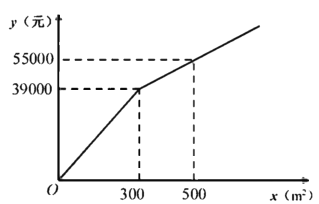
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
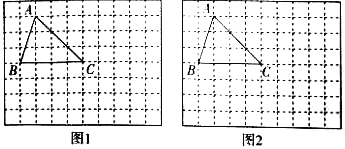
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC(注:顶点在网格线交点处的三角形叫做格点三角形).只用没有刻度的直尺,按如下要求画图,
(1)以点C为位似中心,在如图中作△DEC∽ABC,且相似比为1:2;
(2)若点B为原点,点C(4,0),请在如图中画出平面直角坐标系,作出△ABC的外心,并直接写出△ABC的外心的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com