
分析 (1)直接利用根与系数的关系得出答案即可;
(2)首先转化为两根和与两根积的形式,然后代入求得答案即可.
解答 解:(1)∵关于x的方程x2-x-2=0的两根为x1、x2,
∴x1+x2=1,x1x2=-2;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{1}{-2}$=-$\frac{1}{2}$.
点评 此题考查了根与系数的关系:如果一元二次方程ax2+bx+c=0的两根分别为x1与x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
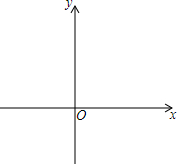 已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.
已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 | B. | 20 | C. | 15 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com