
 已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.
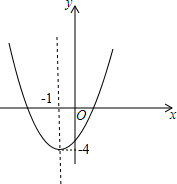
已知函数y=x2+2x-3的图象与x轴交于点A,B(A在B的左侧),与y轴交于点C.分析 (1))画出函数图象,如图所示;
(2)利用平移规律判断即可.
(3)把抛物线y=x2+2x-3整理成顶点式形式并求出顶点坐标,再求出与y轴的交点坐标,然后求出所得抛物线的顶点,再利用顶点式形式写出解析式即可.
解答 (1)y=x2+2x-3=(x+1)2-4,即顶点为(-1,-4),
列表得:
| x | -3 | -2 | -1 | 0 | 1 |
| y | 0 | -3 | -4 | -3 | 0 |
点评 此题主要考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式的变化可以使求解更简便.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com