Question

17．定义正整数m，n的运算：m△n=$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+$\frac{1}{{m}^{4}}$+…+$\frac{1}{{m}^{n}}$
（1）计算3△2的值为$\frac{4}{9}$；运算“△”满足交换规律吗？回答：否（填“是”或“否”）
（2）探究：计算2△10=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{2{0}^{10}}$的值．
为解决上面的问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系的几何图形结合起来，最终解决问题．
如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为$\frac{1}{2}$；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为$\frac{1}{2}$$+\frac{1}{{2}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为$\frac{1}{2}$-$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{10}}$，最后空白部分的面积是$\frac{1}{{2}^{10}}$；根据第10次分割图可以得出计算结果：$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{10}}$=1-$\frac{1}{{2}^{10}}$．
进一步分析可得出，$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$
（3）已知n是正整数，计算4△n=$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+$\frac{1}{{4}^{4}}$+…+$\frac{1}{{4}^{n}}$的结果．
按指定方法解决问题：请仿照以上做法，只需画出第n次分割图并作标注，写出最终结果的推理步骤；或借用以上结论进行推理，写出必要的步骤．

Answer 1

分析 （1）根据新定义运算法则进行计算即可；
（2）根据计算2△10=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{2{\;}^{10}}$的值的计算过程得到规律解题；
（3）根据探究的分割方法依次进行分割，然后表示出阴影部分的面积，再除以3即可．

解答 解：（1）3△2=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$=$\frac{4}{9}$．
而2△3=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$=$\frac{7}{8}$，
则3△2≠2△3，
所以运算“△”不满足交换规律．
故答案是：$\frac{4}{9}$；否；

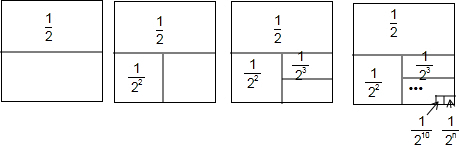
（2）如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为$\frac{1}{2}$；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为$\frac{1}{2}$$+\frac{1}{{2}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为$\frac{1}{2}$-$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{10}}$，最后空白部分的面积是$\frac{1}{{2}^{10}}$；
根据第10次分割图可以得出计算结果：$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{10}}$=1-$\frac{1}{{2}^{10}}$．
进一步分析可得出，$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$．
故答案是：1-$\frac{1}{{2}^{n}}$．

（3）第1次分割，把正方形的面积四等分，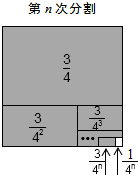

其中阴影部分的面积为$\frac{3}{4}$；
第2次分割，把上次分割图中空白部分的面积继续四等分，
阴影部分的面积之和为$\frac{3}{4}$；
第3次分割，把上次分割图中空白部分的面积继续四等分，
…，
第n次分割，把上次分割图中空白部分的面积最后四等分，
所有阴影部分的面积之和为：$\frac{3}{4}$+$\frac{3}{{4}^{2}}$+$\frac{3}{{4}^{3}}$+…+$\frac{3}{{4}^{n}}$，
最后的空白部分的面积是$\frac{1}{{4}^{n}}$，
根据第n次分割图可得等式：$\frac{3}{4}$+$\frac{3}{{4}^{2}}$+$\frac{3}{{4}^{3}}$+…+$\frac{3}{{4}^{n}}$=1-$\frac{1}{{4}^{n}}$，
两边同除以3，得$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{n}}$=$\frac{1}{3}$-$\frac{1}{3×{4}^{n}}$．

点评 本题考查了应用与设计作图，图形的变化规律，读懂题目信息，理解分割的方法以及求和的方法是解题的关键．