【题目】如图，菱形的对角线BD，AC的长分别是6和8，求菱形的周长与面积．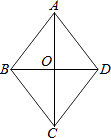 
【答案】解：菱形的对角线BD，AC的长分别是6和8，
则菱形的面积为 
×6×8=24，
菱形对角线互相垂直平分，
∴BO=OD=3，AO=OC=4，
∴AB= 
=5，
故菱形的周长为20，
答：菱形的周长为20，面积为24．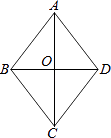
【解析】根据菱形的对角线可以求得菱形ABCD的面积，根据菱形对角线互相垂直平分的性质，可以求得BO=OD，AO=OC，在Rt△AOB中，根据勾股定理可以求得AB的长，即可求菱形ABCD的周长．
【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案科目：初中数学 来源： 题型：
【题目】方程4x2＝81化成一元二次方程的一般形式后，其中的二次项系数、一次项系数和常数项分别是（ ）
A.4，0，81B.﹣4，0，81C.4，0，﹣81D.﹣4，0，﹣81
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支，主干、枝干和小分支的总数是91，设每个枝干长出x小分支，列方程为（ ）
A.（1+x）2＝91B.1+x+x2＝91C.（1+x）x＝91D.1+x+2x＝91
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC的边长为30，点M为线段AB上一动点，将等边△ABC沿过点M的直线折叠，使点A落在直线BC上的点D处，且BD∶DC＝1∶4，折痕与直线AC交于点N，则AN的长为________．
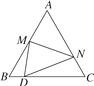
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．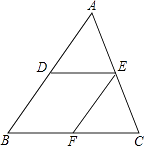 
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1＝∠2，∠3＝∠4，∠BOD＝
∠AOB＝90°．下列判断：①射线OF是∠BOE的角平分线；②∠DOE的补角是∠BOC；③∠AOC的余角只有∠COD；④∠DOE的余角有∠BOE和∠COD；⑤∠COD＝∠BOE．其中正确的有（ ）
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com