
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F. 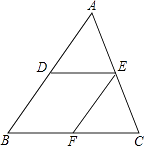
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且![]() .
.
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
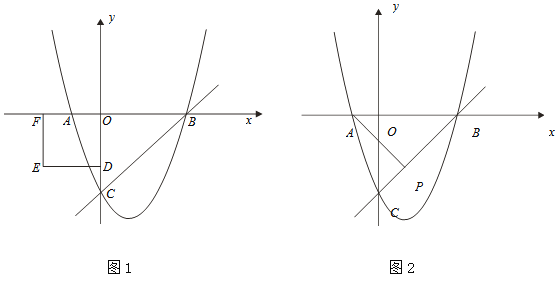
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).求:①s与t之间的函数关系式; ②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光垂直照射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树AC的高度.(结果精确到0.1m.参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳半径约为696000km,将696000用科学记数法表示为( )
A.696×103
B.69.6×104
C.6.96×105
D.0.696×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com