
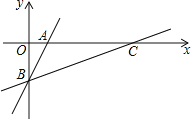
【题目】如图,在平面直角坐标系中,一次函数y=2x﹣1的图象分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是_____.
【答案】y=![]() x﹣1.
x﹣1.
【解析】
根据已知条件得到A(![]() ,0),B(0,﹣1),求得OA=
,0),B(0,﹣1),求得OA=![]() ,OB=1,过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,得到AB=AF,根据全等三角形的性质得到AE=OB=1,EF=OA=
,OB=1,过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,得到AB=AF,根据全等三角形的性质得到AE=OB=1,EF=OA=![]() ,求得F(
,求得F(![]() ,﹣
,﹣![]() ),设直线BC的函数表达式为:y=kx+b,解方程组于是得到结论.
),设直线BC的函数表达式为:y=kx+b,解方程组于是得到结论.
解:∵一次函数y=2x﹣1的图象分别交x、y轴于点A、B,
∴令x=0,得y=﹣1,令y=0,则x=![]() ,
,
∴A(![]() ,0),B(0,﹣1),
,0),B(0,﹣1),
∴OA=![]() ,OB=1,
,OB=1,
过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,
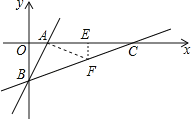
∵∠ABC=45°,
∴△ABF是等腰直角三角形,
∴AB=AF,
∵∠OAB+∠ABO=∠OAB+∠EAF=90°,
∴∠ABO=∠EAF,
∴△ABO≌△FAE(AAS),
∴AE=OB=1,EF=OA=![]() ,
,
∴F(![]() ,﹣
,﹣![]() ),
),
设直线BC的函数表达式为:y=kx+b,
∴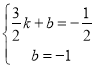 ,
,
∴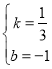 ,
,
∴直线BC的函数表达式为:y=![]() x﹣1,
x﹣1,
故答案为:y=![]() x﹣1.
x﹣1.


科目:初中数学 来源: 题型:
【题目】用一段长32m的篱笆和长8m的墙,围成一个矩形的菜园.
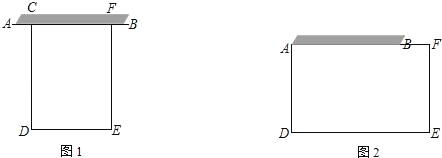
(1)如图1,如果矩形菜园的一边靠墙AB,另三边由篱笆CDEF围成
①设DE等于xm,直接写出菜园面积y与x之间的函数关系式,并写出自变量的取值范围;
②菜园的面积能不能等于110m2?若能,求出此时x的值;若不能,请说明理由;
(2)如图2,如果矩形菜园的一边由墙AB和一节篱笆BF构成,另三边由篱笆ADEF围成,求菜园面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
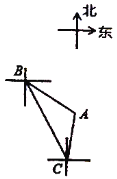
【题目】如图,轮船从![]() 处以每小时60海里的速度沿南偏东
处以每小时60海里的速度沿南偏东![]() 方向匀速航行,在
方向匀速航行,在![]() 处观测灯塔
处观测灯塔![]() 位于南偏东
位于南偏东![]() 方向上,轮船航行40分钟到达
方向上,轮船航行40分钟到达![]() 处,在
处,在![]() 处观测灯塔
处观测灯塔![]() 位于北偏东
位于北偏东![]() 方向上,求
方向上,求![]() 处与灯塔
处与灯塔![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣8.
(1)用配方法把y=x2﹣2x﹣8化为y=(x﹣h)2+k形式;
(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,抛物线与x轴交点坐标是 ,当x 时,y随x的增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
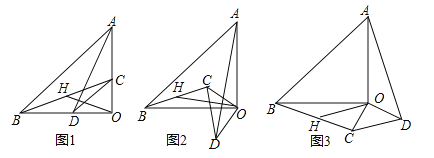
【题目】(2017黑龙江省龙东地区)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
(1)如图1所示,易证:OH=![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
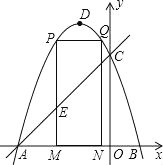
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-(2m-1)x+m2-m(m是常数)
(1)当m=2时,求二次函数图象与x轴的交点;
(2)若A(n-3,n2+2),B(-n+1,n2+2)是该二次函数图象上的两个不同点,求m的值和二次函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com