
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
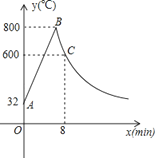
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
【答案】解:(1)停止加热时,设![]() (k≠0),
(k≠0),
由题意得![]() ,解得k=4800。
,解得k=4800。
∴![]() 。
。
当y=800时, ![]() ,解得x=6。∴点B的坐标为(6,800)。
,解得x=6。∴点B的坐标为(6,800)。
材料加热时,设y=ax+32(a≠0),
由题意得800=6a+32,解得a=128。
∴材料加热时,y与x的函数关系式为y=128x+32(0≤x≤6);
停止加热进行操作时y与x的函数关系式为![]() (x>6)。
(x>6)。
(2)把y=480代入![]() ,得x=10,
,得x=10,
∴从开始加热到停止操作,共经历了10分钟。
∵10—6=4(分),
∴锻造的操作时间为4分钟。
【解析】试题分析:(1)根据题意,材料煅烧时,温度![]() 与时间
与时间![]() 成一次函数关系,煅烧结束时,温度
成一次函数关系,煅烧结束时,温度![]() 与
与![]() 时间成反比例函数关系,将题中数据代入,用待定系数法可得两个函数的关系式;
时间成反比例函数关系,将题中数据代入,用待定系数法可得两个函数的关系式;
(2)把![]() 代入
代入![]() 中,求解得出答案即可.
中,求解得出答案即可.
试题解析:(1)停止加热时,设![]() ,由题意得
,由题意得![]() ,解得
,解得![]() ,当
,当![]() 时,
时, ![]() 解得
解得![]() ,点B的坐标为(6,800);材料加热时,设
,点B的坐标为(6,800);材料加热时,设![]() ,由题意得
,由题意得![]() ,解得
,解得![]() .材料加热时,
.材料加热时, ![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,停止加热进行锻造时
,停止加热进行锻造时![]() 与
与![]() 的函数关系式为:
的函数关系式为: ![]() .
.
(2)把![]() 代入
代入![]() 中,得
中,得![]()
![]() 分钟.故锻造的操作时间为4分钟.
分钟.故锻造的操作时间为4分钟.


科目:初中数学 来源: 题型:
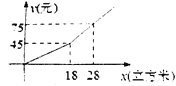
【题目】为了增强人们的节约用水意识,环节城市用水压力。某市规定,每月用水18立方米以内(含18立方米)和用水18立方米以上采取两种不同的收费标准.下图为该市的用户每月应交水费y(元)关于用水量x(立方米)的函数图像.思考并回答下列问题:
(1)求出用水量小于18立方米时,每月应交水费y(元)关于用水量x(立方米)的函数表达式.
(2)若小明家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077m.0.0000077用科学记数法表示是( )
A. 0.77×10﹣5 B. 0.77×10﹣6 C. 7.7×10﹣5 D. 7.7×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=70°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠BEO的度数是( )
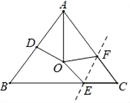
A. 20° B. 35° C. 40° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几组长度的3条线段能构成直角三角形的有( )
①3,4,5;②4,5,6; ③1.5,2,2.5;④8,15,17;⑤5,8,17.
A. ①②④ B. ②④⑤ C. ①③⑤ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com