
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE.点F,点E关于直线AC成轴对称,连接AE,顺次连接AD,DF,AF.


(1)如图1,若点D、点E在边BC上,试判断∠BAD与∠FDC的大小关系,并说明理由;
(2)若点D、点E在边BC所在的直线上如图(2)所示的位置,(1)中的结论是否还成立,说明理由.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型机 | 100 | 60 |
乙型机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ![]() .
.
其中正确的结论有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
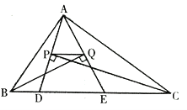
【题目】如图,△ABC的周长为30cm,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=11cm,则DE的长为____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角![]() 中,
中,![]() ,若想找一点P,使得
,若想找一点P,使得![]() 与
与![]() 互补,甲、乙、丙三人作法分别如下:
互补,甲、乙、丙三人作法分别如下:
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和![]() 的平分线,两线交于P点,则P即为所求.
的平分线,两线交于P点,则P即为所求.
对于甲、乙、丙三人的作法,下列叙述正确的是![]()
![]()

A. 三人皆正确B. 甲、丙正确,乙错误
C. 甲正确,乙、丙错误D. 甲错误,乙、丙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期日早晨,小青从家出发匀速去森林公园溜冰,小青出发一段时间后,他妈妈发现小青忘带了溜冰鞋,于是立即骑自行车沿小青行进的路线匀速去追赶,妈妈追上小青后,立即沿原路线匀速返回家,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的三分之二,小青继续以原速度步行前往森林公园,妈妈与小青之间的路程![]() 米
米![]() 与小青从家出发后步行的时间
与小青从家出发后步行的时间![]() 分
分![]() 之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米
之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一只电子狗从原点O出发,按向上→向右→向下→向下→向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,则A3020的坐标为( )

A.(1007,1)B.(1007,﹣1)C.(504,1)D.(504,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD被两条与边平行的线段EF,GH分割成四个小长方形,EF与GH交于点P,设BF长为a,BG长为b,△GBF的周长为m,
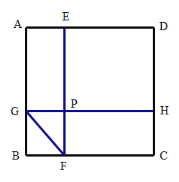
(1)①用含a,b,m的式子表示GF的长为 ;
②用含a,b的式子表示长方形EPHD的面积为 ;
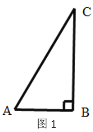
(2)已知直角三角形两直角边的平方和等于斜边的平方,
例如在图1,△ABC中,∠ABC=900,则![]() ,
,
请用上述知识解决下列问题:
①写出a,b,m满足的等式 ;
②若m=1,求长方形EPHD的面积;
③当m满足什么条件时,长方形EPHD的面积是一个常数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com