Question

【题目】如图，边长为1的正方形ABCD被两条与边平行的线段EF，GH分割成四个小长方形，EF与GH交于点P，设BF长为a，BG长为b，△GBF的周长为m，

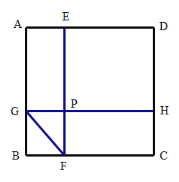
(1)①用含a，b，m的式子表示GF的长为 ；

②用含a，b的式子表示长方形EPHD的面积为 ；

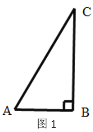
(2)已知直角三角形两直角边的平方和等于斜边的平方，

例如在图1，△ABC中，∠ABC=900，则，

请用上述知识解决下列问题：

①写出a，b，m满足的等式 ；

②若m=1，求长方形EPHD的面积；

③当m满足什么条件时，长方形EPHD的面积是一个常数？

Answer 1

【答案】（1）①；②；（2）①；②；③m=1

【解析】

（1）①直接根据三角形的周长公式即可；

②根据BF长为a，BG长为b，表示出EP，PH的长，根据求长方形EPHD的面积；

（2）①直接根据直角三角形两直角边的平方和等于斜边的平方，表示出a，b，m之间的关系式；

②根据线段之间的关系利用勾股定理求出长方形EPHD的面积的值；

③结合①的结论和②的作法即可求解.

（1）①∵BF长为a，BG长为b，△GBF的周长为m，

∴，

故答案为：；

②∵正方形ABCD的边长为1 ，

∴AB=BC=1，

∵BF长为a，BG长为b，

∴AG=1-b，FC=1-a，

∴EP=AG=1-b，PH=FC=1-a，

∴长方形EPHD的面积为：，

故答案为：；

（2）①△ABC中，∠ABC=90°，则，

∴在△GBF中， ，

∴，

化简得，

故答案为：；

②∵BF=a，GB=b，

∴FC=1-a，AG=1-b，

在Rt△GBF中，，

∵Rt△GBF的周长为1，

∴

即 ，

即，

整理得

∴，

∴矩形EPHD的面积

．

③由①得： ，

∴.

∴矩形EPHD的面积

，

∴要使长方形EPHD的面积是一个常数，只有m=1．