
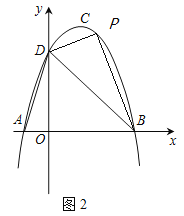
【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
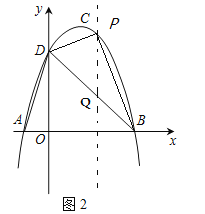
(2)如图2,点P为直线BD上方抛物线上一点,若![]() ,请求出点P的坐标.
,请求出点P的坐标.
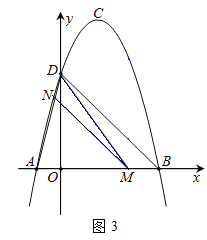
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.

【答案】(1)y=-x2+2x+3;(2)点P的坐标为(1,4)或(2,3);(3)点M的坐标为(![]() ,0).
,0).
【解析】
(1)设抛物线的解析式为:y=a(x-1)2+4,然后将点B的坐标代入函数解析式即可求得此抛物线的解析式;
(2)如图2,过点P作PQ//y轴交DB于Q,求出直线BD的解析式,设P(m, -m2+2m+3),则Q(m,-m+3),得到S△PBD =-![]() m2+
m2+![]() m,又
m,又![]() ,解方程求出m的值,再求点P的坐标即可;
,解方程求出m的值,再求点P的坐标即可;
(3)设M(c,0),由△AMN∽△AMD,得到![]() ,得出MN=
,得出MN=![]() ,DM=
,DM=![]() ,再由△DNM∽△BMD,得到
,再由△DNM∽△BMD,得到![]() ,即9+c2=
,即9+c2=![]() ×
×![]() ,求解即可的出答案.
,求解即可的出答案.
(1)设所求抛物线的解析式为:y=a(x-1)2+4,
将点B(3,0)代入,得:(3-1)2a+4=0
解得:a=-1
∴解析式为:y=-(x-1)2+4=-x2+2x+3
(2)如图2,过点P作PQ//y轴交DB于Q,
∵抛物线的解析式为y=-x2+2x+3,
∴点D的坐标为(0,3),
设直线BD的解析式为y=kx+b,
把D(0,3)和B(3,0)代入y=kx+b得,![]() ,
,
解得:![]()
∴直线BD的解析式为y=-x+3,
设P(m, -m2+2m+3),则Q(m,-m+3).
∴PQ=-m2+2m+3(-m+3)= -m2+3m,
又∵S△PBD=S△PQD+S△PQB
=![]() mPQ+
mPQ+![]() (3m)PQ=
(3m)PQ=![]() PQ×3=
PQ×3=![]() PQ=-
PQ=-![]() m
m![]() m,
m,
∵![]() ,
,
∴-![]() m2+
m2+![]() m=3
m=3
解得:m1=1,m2=2,
∴点P的坐标为(1,4)或(2,3)
(3) ∵BD=![]() ,设M(c,0),
,设M(c,0),
∵MN∥BD,
∴△AMN∽△AMD,
∴![]() ,即
,即![]() ,
,
∴MN=![]() ,DM=
,DM=![]() ,
,
∵△DNM∽△BMD,
∴![]() ,即DM2=BD·MN,
,即DM2=BD·MN,
∴9+c2=![]() ×
×![]() ,
,
解得:c=![]() 或c=3(舍去),
或c=3(舍去),
∴点M的坐标为(![]() ,0).
,0).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C(0,![]() ),顶点为D,对称轴交x轴于点E.
),顶点为D,对称轴交x轴于点E.
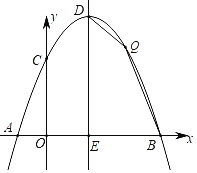
(1)求该抛物线的一般式;
(2)若点Q为该抛物线上第一象限内一动点,且点Q在对称轴DE的右侧,求四边形DEBQ面积的最大值及此时点Q的坐标;
(3)若点P为对称轴DE上异于D,E的动点,过点D作直线PB的垂线交直线PB于点F,交x轴于点G,当△PDG为等腰三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篮球运动是全世界最流行的运动之一,近年流行于青少年之间的“3对3”篮球将登上2020年奥运会赛场,为备战某市中学生“3对3”篮球联赛,某校甲、乙、丙三位同学作为“兄弟战队”的主力队员进行篮球传球训练,篮球由一个人随机传给另一个人,且每位传球人传球给其余两人的机会是均等的,现在由甲开始传球.
(1)求甲第一次传球给乙的概率;
(2)三次传球后,篮球在谁手中的可能性大?请利用树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
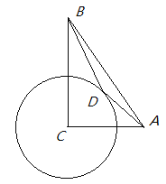
【题目】如图,已知AC=6,BC=8,AB=10,以点C为圆心,4为半径作圆.点D是⊙C上的一个动点,连接AD、BD,则AD+![]() BD的最小值为__________.
BD的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
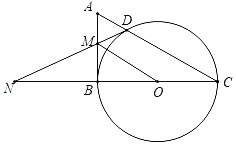
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
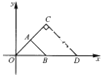
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
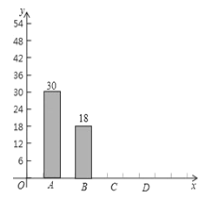
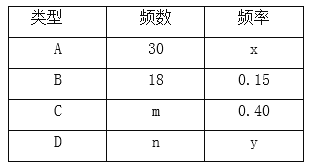
【题目】泉州市某学校抽样调查学生上学的交通工具,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
(1)学生共 人,x= ,y= ;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com