
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ![]() ЃЉЃЌЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкЕуEЃЎ
ЃЉЃЌЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкЕуEЃЎ
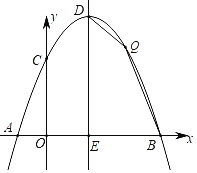
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФвЛАуЪНЃЛ
ЃЈ2ЃЉШєЕуQЮЊИУХзЮяЯпЩЯЕквЛЯѓЯоФквЛЖЏЕуЃЌЧвЕуQдкЖдГЦжсDEЕФгвВрЃЌЧѓЫФБпаЮDEBQУцЛ§ЕФзюДѓжЕМАДЫЪБЕуQЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуPЮЊЖдГЦжсDEЩЯвьгкDЃЌEЕФЖЏЕуЃЌЙ§ЕуDзїжБЯпPBЕФДЙЯпНЛжБЯпPBгкЕуFЃЌНЛxжсгкЕуGЃЌЕБЁїPDGЮЊЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌQЃЈ
ЃЌQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊЃЈ2ЃЌЉ
ЃЉЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊЃЈ2ЃЌЉ![]() ЃЉЛђЃЈ2ЃЌ
ЃЉЛђЃЈ2ЃЌ![]() Љ2ЃЉЛђЃЈ2ЃЌЉ
Љ2ЃЉЛђЃЈ2ЃЌЉ![]() Љ2ЃЉЛђЃЈ2ЃЌЉ
Љ2ЃЉЛђЃЈ2ЃЌЉ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋAЃЌBЃЌCШ§ЕуЕФзјБъжБНгДњШыНтЮіЪНМДПЩЧѓГіaЁЂbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉЙ§ЕуQзїyжсЕФЦНааЯпНЛBDгкЕуMЃЌЩшЕуQЃЈmЃЌ![]() ЃЉЃЌЧѓГіжБЯпBDЕФНтЮіЪНЮЊyЃН
ЃЉЃЌЧѓГіжБЯпBDЕФНтЮіЪНЮЊyЃН![]() ЃЌПЩЩшMЃЈmЃЌ
ЃЌПЩЩшMЃЈmЃЌ![]() ЃЉЃЌдђQMЃН
ЃЉЃЌдђQMЃН![]() ЃЌИљОнSЫФБпаЮDEBQЃНSЁїDEB+SЁїDQM+SЁїBQMПЩЕУГіmЕФБэДяЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЧѓГіД№АИЃЎ
ЃЌИљОнSЫФБпаЮDEBQЃНSЁїDEB+SЁїDQM+SЁїBQMПЩЕУГіmЕФБэДяЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЧѓГіД№АИЃЎ
ЃЈ3ЃЉЩшЕуPЃЈ2ЃЌnЃЉЃЌПЩЕУГіЕуGЃЈ2Љ![]() ЃЌ0ЃЉЃЌЗжЕБGPЃНGDЁЂGPЃНPDЁЂGDЃНPDШ§жжЧщПіЃЌЕУГіnЕФЗНГЬЗжБ№ЧѓНтМДПЩЃЎ
ЃЌ0ЃЉЃЌЗжЕБGPЃНGDЁЂGPЃНPDЁЂGDЃНPDШ§жжЧщПіЃЌЕУГіnЕФЗНГЬЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉАбAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ![]() ЃЉЃЌДњШыХзЮяЯпНтЮіЪНЕУЃК
ЃЉЃЌДњШыХзЮяЯпНтЮіЪНЕУЃК
 ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊЃКyЃНЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпХзЮяЯпНтЮіЪНЮЊyЃНЉ![]() ЃНЉ
ЃНЉ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖЅЕуDЕФзјБъЮЊЃЈ2ЃЌ![]() ЃЉЃЌЖдГЦжсЮЊxЃН2ЃЌEЃЈ2ЃЌ0ЃЉЃЌ
ЃЉЃЌЖдГЦжсЮЊxЃН2ЃЌEЃЈ2ЃЌ0ЃЉЃЌ
Й§ЕуQзїyжсЕФЦНааЯпНЛBDгкЕуMЃЌЩшЕуQЃЈmЃЌ![]() ЃЉЃЌ
ЃЉЃЌ

ЩшжБЯпBDЕФНтЮіЪНЮЊyЃНkx+bЃЌ
дђ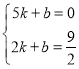 ЃЌ
ЃЌ
НтЕУЃК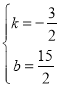 ЃЌ
ЃЌ
ЁржБЯпBDЕФНтЮіЪНЮЊyЃН![]() ЃЌ
ЃЌ
ПЩЩшMЃЈmЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрQMЃН![]() ЉЃЈ
ЉЃЈ![]() ЃЉЃН
ЃЉЃН![]() ЃЌ
ЃЌ
ЁрSЫФБпаЮDEBQЃНSЁїDEB+SЁїDQM+SЁїBQM
ЃН![]() +
+![]() ЁСЃЈmЉ2ЃЉ+
ЁСЃЈmЉ2ЃЉ+![]() ЃЌ
ЃЌ
ЃН![]() ЃЎ
ЃЎ
ЕБmЃН![]() ЪБЃЌSЫФБпаЮDEBQШЁЕУзюДѓжЕЃЌSЫФБпаЮDEBQЃН
ЪБЃЌSЫФБпаЮDEBQШЁЕУзюДѓжЕЃЌSЫФБпаЮDEBQЃН![]() ЃЎ
ЃЎ
ДЫЪБ![]() ЃЎ
ЃЎ
ЁрQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉХзЮяЯпЕФЖдГЦжсЮЊxЃН2ЃЌдђЕуDЃЈ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшЕуPЃЈ2ЃЌnЃЉЃЌ
НЋЕуPЁЂBЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЃКyЃНsx+tВЂНтЕУЃК
КЏЪ§PBЕФБэДяЪНЮЊЃКyЃН![]() ЃЌ
ЃЌ
ЁпDGЁЭPBЃЌ
ЙЪжБЯпDGБэДяЪНжаЕФkжЕЮЊ![]() ЃЌ
ЃЌ
НЋЕуDЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЃЌ
ЭЌРэПЩЕУжБЯпDGЕФБэДяЪНЮЊЃКyЃН![]() ЃЌ
ЃЌ
НтЕУЃКxЃН2Љ![]() ЃЌ
ЃЌ
ЙЪЕуGЃЈ2Љ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрGP2ЃН![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЂйЕБGPЃНGDЪБЃЌ![]()
![]() ЃЌ
ЃЌ
НтЕУЃКnЃНЉ![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрPЃЈ2ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЂкЕБGPЃНPDЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃКnЃНЉ2ЁР![]() ЃЌ
ЃЌ
ЁрPЃЈ2ЃЌЉ2+![]() ЃЉЛђPЃЈ2ЃЌЉ2Љ
ЃЉЛђPЃЈ2ЃЌЉ2Љ![]() ЃЉЃЎ
ЃЉЃЎ
ЂлЕБGDЃНPDЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃКnЃНЉ![]() ЛђnЃН0ЃЈЩсШЅЃЉЃЎ
ЛђnЃН0ЃЈЩсШЅЃЉЃЎ
ЁрPЃЈ2ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злКЯЩЯЪіЃЌЕуPЕФзјБъЮЊЃЈ2ЃЌЉ![]() ЃЉЛђЃЈ2ЃЌ
ЃЉЛђЃЈ2ЃЌ![]() Љ2ЃЉЛђЃЈ2ЃЌЉ
Љ2ЃЉЛђЃЈ2ЃЌЉ![]() Љ2ЃЉЛђЃЈ2ЃЌЉ
Љ2ЃЉЛђЃЈ2ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ


 ПьРж5Мг2Н№ОэЯЕСаД№АИ
ПьРж5Мг2Н№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
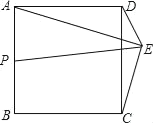
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2![]() ЃЌЕуEЮЊе§ЗНаЮЭтвЛИіЖЏЕуЃЌЁЯAEDЃН45ЁуЃЌPЮЊABжаЕуЃЌЯпЖЮPEЕФзюДѓжЕЪЧ_____ЃЎ
ЃЌЕуEЮЊе§ЗНаЮЭтвЛИіЖЏЕуЃЌЁЯAEDЃН45ЁуЃЌPЮЊABжаЕуЃЌЯпЖЮPEЕФзюДѓжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЁАђдСњЁБКХЩюЧБЦїФПЧАзюДѓЩюЧБМЋЯоЮЊ7062ЃЎ68УзЃЎФГЬьИУЩюЧБЦїдкКЃУцЯТ1800УзДІзївЕЃЈШчЭМЃЉЃЌВтЕУе§ЧАЗНКЃЕзГСДЌCЕФИЉНЧЮЊ45ЁуЃЌИУЩюЧБЦїдкЭЌвЛЩюЖШЯђе§ЧАЗНжБЯпКНаа2000УзЕНBЕуЃЌДЫЪБВтЕУКЃЕзГСДЌCЕФИЉНЧЮЊ60ЁуЃЎЧыХаЖЯГСДЌCЪЧЗёдкЁАђдСњЁБКХЩюЧБМЋЯоЗЖЮЇФкЃПВЂЫЕУїРэгЩЃЛЃЈОЋШЗЕН0ЃЎ01ЃЉЃЈВЮПМЪ§ОнЃК![]() Ёж1ЃЎ414ЃЌ
Ёж1ЃЎ414ЃЌ![]() Ёж1ЃЎ732ЃЉ
Ёж1ЃЎ732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
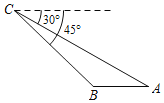
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуCДІгавЛИіИпПеЬНВтЦјЧђЃЌДгЕуCДІВтЕУЫЎЦНЕиУцЩЯAЃЌBСНЕуЕФИЉНЧЗжБ№ЮЊ30ЁуКЭ45ЁуЃЎШєAB=2kmЃЌдђAЃЌCСНЕужЎМфЕФОрРыЮЊ_____kmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯDЃН90ЁуЃЌADЃН4ЃЌBCЃН3ЃЎЗжБ№вдЕуAЃЌCЮЊдВаФЃЌДѓгк![]() ACГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуEЃЌЩфЯпBEНЛADгкЕуFЃЌНЛACгкЕуOЃЎШєЕуOЧЁКУЪЧACЕФжаЕуЃЌдђCDЕФГЄЮЊ__ЃЎ
ACГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуEЃЌЩфЯпBEНЛADгкЕуFЃЌНЛACгкЕуOЃЎШєЕуOЧЁКУЪЧACЕФжаЕуЃЌдђCDЕФГЄЮЊ__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
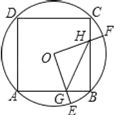
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ2ЕФе§ЗНаЮABCDФкНггкЁбOЃЌЕуEЪЧ![]() ЩЯвЛЕуЃЈВЛгыAЁЂBжиКЯЃЉЃЌЕуFЪЧ
ЩЯвЛЕуЃЈВЛгыAЁЂBжиКЯЃЉЃЌЕуFЪЧ![]() ЩЯвЛЕуЃЌСЌНгOEЃЌOFЃЌЗжБ№гыABЃЌBCНЛгкЕуGЃЌBЃЌЧвЁЯEOFЃН90ЁуЃЎгаЯТСаНсТлЃКЂй
ЩЯвЛЕуЃЌСЌНгOEЃЌOFЃЌЗжБ№гыABЃЌBCНЛгкЕуGЃЌBЃЌЧвЁЯEOFЃН90ЁуЃЎгаЯТСаНсТлЃКЂй![]() ЃН
ЃН![]() ЃЛЂкЫФБпаЮOGBHЕФУцЛ§ЫцзХЕуEЮЛжУЕФБфЛЏЖјБфЛЏЃЛЂлЁїGBHжмГЄЕФзюаЁжЕЮЊ2+
ЃЛЂкЫФБпаЮOGBHЕФУцЛ§ЫцзХЕуEЮЛжУЕФБфЛЏЖјБфЛЏЃЛЂлЁїGBHжмГЄЕФзюаЁжЕЮЊ2+![]() ЃЛЂмШєBGЃН1Љ
ЃЛЂмШєBGЃН1Љ![]() ЃЌдђBGЃЌGEЃЌ
ЃЌдђBGЃЌGEЃЌ![]() ЮЇГЩЕФУцЛ§ЪЧ
ЮЇГЩЕФУцЛ§ЪЧ![]() ЃЌЦфжае§ШЗЕФЪЧ_____ЃЎЃЈАбЫљгае§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ЃЌЦфжае§ШЗЕФЪЧ_____ЃЎЃЈАбЫљгае§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌADЃНBDЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌЙ§ЕуAзїAHЁЭBDгкЕуHЃЌНЛDEЁЂBCЗжБ№гкЕуFЁЂGЃЌСЌНгCFЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЁЯBAGЃНЁЯFCBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуAзїAKЦНЗжЁЯDAFНЛEDгкЕуKЃЌШєAKЃН1ЃЌЁЯFCDЃН45ЁуЃЌЧѓDFЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєADЃН10ЃЌDHЃН6ЃЌЧѓCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтЦпЁЂАЫФъМЖбЇЩњЖдЁАЗРФчЫЎЁБАВШЋжЊЪЖЕФеЦЮеЧщПіЃЌДгЦпЁЂАЫФъМЖИїЫцЛњГщШЁ50УћбЇЩњНјааВтЪдЃЌВЂЖдГЩМЈЃЈАйЗжжЦЃЉНјааећРэЁЂУшЪіКЭЗжЮіЃЎВПЗжаХЯЂШчЯТЃК
aЃЎЦпФъМЖГЩМЈЦЕЪ§ЗжВМжБЗНЭМЃК

bЃЎЦпФъМЖГЩМЈдк![]() етвЛзщЕФЪЧЃК70 72 74 75 76 76 77 77 77 78 79
етвЛзщЕФЪЧЃК70 72 74 75 76 76 77 77 77 78 79
cЃЎЦпЁЂАЫФъМЖГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ШчЯТЃК
ФъМЖ | ЦНОљЪ§ | жаЮЛЪ§ |
Цп | 76.9 | m |
АЫ | 79.2 | 79.5 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкетДЮВтЪджаЃЌЦпФъМЖдк80ЗжвдЩЯЃЈКЌ80ЗжЃЉЕФгаЁЁ ЁЁШЫЃЛ
ЃЈ2ЃЉБэжаmЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉдкетДЮВтЪджаЃЌЦпФъМЖбЇЩњМзгыАЫФъМЖбЇЩњввЕФГЩМЈЖМЪЧ78ЗжЃЌЧыХаЖЯСНЮЛбЇЩњдкИїздФъМЖЕФХХУћЫИќППЧАЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ4ЃЉИУаЃЦпФъМЖбЇЩњга400ШЫЃЌМйЩшШЋВПВЮМгДЫДЮВтЪдЃЌЧыЙРМЦЦпФъМЖГЩМЈГЌЙ§ЦНОљЪ§76.9ЗжЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
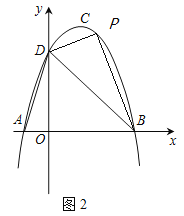
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕуЮЊC(1ЃЌ4)ЃЌНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуDЃЌЦфжаЕуBЕФзјБъЮЊ(3ЃЌ0)ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЮЊжБЯпBDЩЯЗНХзЮяЯпЩЯвЛЕуЃЌШє![]() ЃЌЧыЧѓГіЕуPЕФзјБъЃЎ
ЃЌЧыЧѓГіЕуPЕФзјБъЃЎ
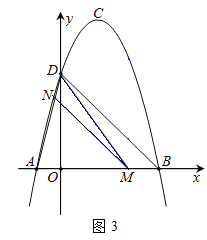
ЃЈ3ЃЉШчЭМ3ЃЌMЮЊЯпЖЮABЩЯЕФвЛЕуЃЌЙ§ЕуMзїMNЁЮBDЃЌНЛЯпЖЮADгкЕуNЃЌСЌНгMDЃЌШєЁїDNMЁзЁїBMDЃЌЧыЧѓГіЕуMЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com