
【题目】已知m,n(m<n)是关于x的方程(x–a)(x–b)=2的两根,若a<b,则下列判断正确的是
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P是第一象限角平分线上的一点,OP=![]() ,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点
,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点

(1)求点P的坐标
(2)若点A的坐标为(0,m),点B的坐标为(n,0),试判断m、n有什么数量关系,并说明理由
(3)连接AB,△ABO的面积是否存在最大值,若存在,求出最大值,若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是______________.
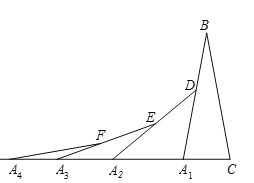
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第![]() 天生产空调
天生产空调![]() 台,直接写出
台,直接写出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:大家知道![]() 是无理数是无限不循环小数,因此
是无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分。又例如:因为
的整数部分是1,将这个数减去其整数部分,差就是小数部分。又例如:因为![]() ,即
,即![]() ,所以
,所以![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ,请解答下列问题:
,请解答下列问题:
(1) 如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求
的整数部分为b,求![]() 的值;
的值;
(2)已知![]() ,其中x是整数,且
,其中x是整数,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | |||
乙 | 80 | 1060 |
(2)请回答下面问题
①从平均数和中位数来分析,甲,乙两城市的空气质量.
②从平均数和方差来分析,甲,乙两城市的空气质量情况.
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com