
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④2CD2=CEAB.其中正确结论的序号是 . 
【答案】①④
【解析】解:①∵AB是半圆直径, ∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO= ![]() ∠CAB,
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴①正确.
②过点E作EF⊥AC,
∵OC⊥AB,AD平分∠CAB交弧BC于点D,
∴OE=EF,
在Rt△EFC中,CE>EF,
∴CE>OE,
∴②错误.
③∵在△ODE和△ADO中,只有∠ADO=∠EDO,
∵∠COD=2∠CAD=2∠OAD,
∴∠DOE≠∠DAO,
∴不能证明△ODE和△ADO相似,
∴③错误;
④∵AD平分∠CAB交弧BC于点D,
∴∠CAD= ![]() ×45°=22.5°,
×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证),
∴∠CDE=∠ODC﹣∠ADO=67.5°﹣22.5°=45°,
∴△CED∽△CDO,
∴ ![]() ,
,
∴CD2=OCCE= ![]() ABCE,
ABCE,
∴2CD2=CEAB.
∴④正确.
综上所述,只有①④正确.
所以答案是:①④.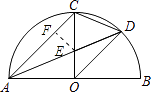
【考点精析】根据题目的已知条件,利用三角形的内角和外角和等腰三角形的判定的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,D点在抛物线y= ![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= ![]() ,M是抛物线与y轴的交点.
,M是抛物线与y轴的交点.
(1)求直线AC和抛物线的解析式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动.问:当P运动到何处时,△APQ是直角三角形?
(3)在(2)中当P运动到某处时,四边形PDCQ的面积最小,求此时△CMQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )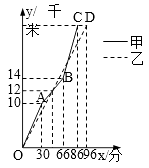
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8cm,E、F、G分别是AB、CD、DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)判断直线EG是否经过某一定点,说明理由;
(3)求四边形EFGH面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC. 
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC= ![]() ,tan∠AEC=
,tan∠AEC= ![]() ,求圆的直径.
,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).
(1)请根据图1,回答下列问题:
①这个班共有名学生,发言次数是5次的男生有人、女生有人;
②男、女生发言次数的中位数分别是次和次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)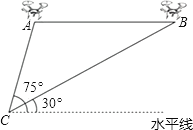
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点
(1)求此抛物线的解析式;
(2)若把抛物线y=ax2+bx+c(a≠0)向下平移 ![]() 个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com