
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )
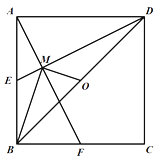
A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
【答案】C
【解析】根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,从而判断①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得![]() =
=![]() =
=![]() =2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
=2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°.
∵E、F分别为边AB,BC的中点,∴AE=BF=![]() BC.在△ABF和△DAE中,
BC.在△ABF和△DAE中,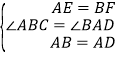 ,∴△ABF≌△DAE(SAS),∴∠BAF=∠ADE.
,∴△ABF≌△DAE(SAS),∴∠BAF=∠ADE.
∵∠BAF+∠DAF=∠BAD=90°,∴∠ADE+∠DAF=∠BAD=90°,∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;
∵DE是△ABD的中线,∴∠ADE≠∠EDB,∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,∴△AED∽△MAD∽△MEA,∴![]() =
=![]() =
=![]() =2,∴AM=2EM,MD=2AM,∴MD=2AM=4EM,故④正确;
=2,∴AM=2EM,MD=2AM,∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a.在Rt△ABF中,AF=![]() =
=![]() =
=![]() a.
a.
∵∠BAF=∠MAE,∠ABC=∠AME=90°,∴△AME∽△ABF,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得AM=
,解得AM=![]() a,∴MF=AF﹣AM=
a,∴MF=AF﹣AM=![]() a﹣
a﹣![]() a=
a=![]() a,∴AM=
a,∴AM=![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,则![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,解得MN=
,解得MN=![]() a,AN=
a,AN=![]() a,∴NB=AB﹣AN=2a﹣
a,∴NB=AB﹣AN=2a﹣![]() a=
a=![]() a,根据勾股定理,BM=
a,根据勾股定理,BM=![]() =
=![]() =
=![]() a,过点M作GH∥AB,过点O作OK⊥GH于K,则OK=a﹣
a,过点M作GH∥AB,过点O作OK⊥GH于K,则OK=a﹣![]() a=
a=![]() a,MK=
a,MK=![]() a﹣a=
a﹣a=![]() a.在Rt△MKO中,MO=
a.在Rt△MKO中,MO=![]() =
=![]() =
=![]() a,根据正方形的性质,BO=2a×
a,根据正方形的性质,BO=2a×![]() =
=![]() a.
a.
∵BM2+MO2=(![]() a)2+(
a)2+(![]() a)2=2a2,BO2=(
a)2=2a2,BO2=(![]() a)2=2a2,∴BM2+MO2=BO2,∴△BMO是直角三角形,∠BMO=90°,故③正确;
a)2=2a2,∴BM2+MO2=BO2,∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述:正确的结论有①③④⑤.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“互异数”,将一个“互异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“互异数”,将一个“互异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() =123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以![]() =6.
=6.
(1)计算![]() 和
和![]() 的值,你发现了什么规律?请用自己的语言表达;
的值,你发现了什么规律?请用自己的语言表达;
(2)若![]() =7,请直接写出
=7,请直接写出![]() 的最小值;
的最小值;
(3)若![]() ,
,![]() 都是“互异数”,其中
都是“互异数”,其中![]() ,
,![]() (1≤
(1≤![]() ≤9,1≤
≤9,1≤![]() ≤9,
≤9,![]() ,
,![]() 都是正整数),当
都是正整数),当![]() +
+![]() =16时,求
=16时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
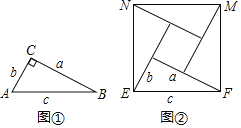
【题目】如图①,在Rt△ABC中,∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)若Rt△ABC的两直角边之比均为2:3.现随机向该图形内掷一枚小针,则针尖落在四个直角三角形区域的概率是多少?
(2)若正方形EFMN的边长为8,Rt△ABC的周长为18,求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
商店经营有A、B两种品牌的笔,A种笔的单价比B种笔的单价贵2元,若花140买A种笔,120元买B种笔,则A种笔反而比B种笔少一支.
(1)求A、B两种品牌的笔每支各多少元.
(2)某单位准备一次性购买两种笔共200支,预计费用不超过1800元.并且规定,A种笔的数量不能少于B种笔的![]() .问如何购买,单位花钱最少?最少花多少钱?
.问如何购买,单位花钱最少?最少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
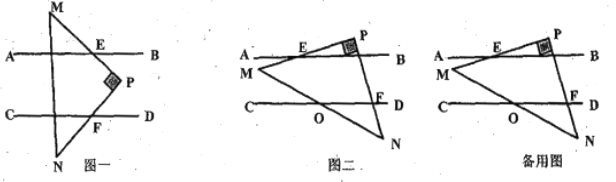
(1)当![]() 所放位置如图一所示时,则
所放位置如图一所示时,则![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(2)当![]() 所放位置如图二所示时,试说明:
所放位置如图二所示时,试说明:![]() ;
;
(3)在(2)的条件下,若![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为提高学生的身体素质,经常在课间开展学生跳绳比赛,下表为该校七年级![]() 班
班![]() 名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟
名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟![]() 个.
个.
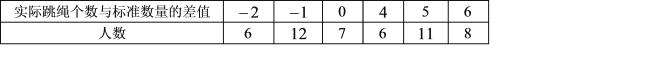
(1)求七年级![]() 班
班![]() 人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
(2)跳绳比赛的计分方式如下:
①若每分钟跳绳个数是规定标准数量,不计分;
②若每分钟跳绳个数超过规定标准数量,每多跳![]() 个绳加
个绳加![]() 分
分
③若每分钟跳绳个数没有达到规定标准数量,每少跳![]() 个绳扣
个绳扣![]() 分
分
如果班级跳绳总积分超过![]() 分,便可得到学校的奖励,请你通过计算说明七年级
分,便可得到学校的奖励,请你通过计算说明七年级![]() 班能否得到学校奖励?
班能否得到学校奖励?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com