练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

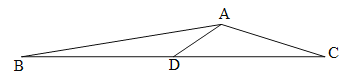
    【题目】如图，在△ABC中，AD是BC边上的中线，∠BAC=150，∠CAD=120．求证：AC=2AD．

    【答案】证明见解析．

    【解析】

    延长AD到E，使DE=AD，连接EC．通过SAS证明△ABD≌△ECD，得到∠BAD=∠E=30°，根据三角形内角和定理得到∠ACE=30°，由等角对等边得到AE=AC，即可得到结论．

    延长AD到E，使DE=AD，连接EC．

    ∵BD=CD，∠BDA=∠CDE，AD=ED，∴△ABD≌△ECD，∴∠BAD=∠E．

    ∵∠BAC=150°，∠CAD=120°，∴∠BAD=150°－120°=30°，∴∠E=30°，∴∠ACE=180°－120°－30°=30°，∴∠E=∠ACE，∴AE=AC，∴AC=2AD．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

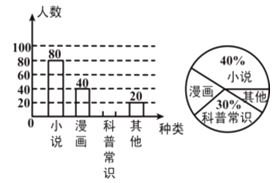
    【题目】某校为了了解本校七年级学生课外阅读的喜好，随机抽取该校七年级部分学生进行问卷调査（每人只选一种书籍）．下图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

    （1）在扇形统计图中，“其他”所在扇形的圆心角等于 度；

    （2）若该年级有600名学生，请你估计该年级喜欢“科普常识”的学生人数约是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程．

    （1）

    （2）

    （3）

    （4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D竖起标杆DE，使得点E与点C、A共线．

    已知：CB⊥AD，ED⊥AD，测得BC＝1m，DE＝1.5m，BD＝8.5m．测量示意图如图所示．请根据相关测量信息，求河宽AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在复习课上，wsy老师要求写出几个与实数有关的结论：小明同学写了以下5个：

    ①任何无理数都是无限不循环小数；

    ②有理数与数轴上的点一一对应；

    ③在1和3之间的无理数有且只有这5个；

    ④是分数，它是有理数；

    ⑤由四舍五入得到的近似数7.30表示大于或等于7.295，而小于7.305的数．其中正确的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知E,F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤AM=MF.其中正确结论的是（ ）

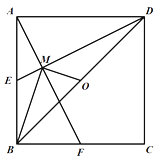
    A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD⊥CD，BC⊥CD，E为CD的中点，连接AE，BE，BE⊥AE，延长AE交BC的延长线于点F。

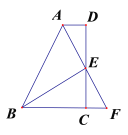
    证明：（1）FC=AD；

    （2）AB=BC+AD。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点D、F、E、G都在△ABC的边上，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数．（请在下面的空格处填写理由或数学式）

    解：∵EF∥AD，（已知）

    ∴∠2=　 　（　 　）

    ∵∠1=∠2，（已知）

    ∴∠1=　 　（　 　）

    ∴　 　∥　 　，（　 　）

    ∴∠AGD+　 　=180°，（两直线平行，同旁内角互补）

    ∵　 　，（已知）

    ∴∠AGD=　 　（等式性质）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

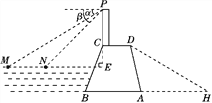
    【题目】某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD.大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．

    （1）求两渔船M，N之间的距离(结果精确到1米)．

    （2）已知坝高24米，坝长100米，背水坡AD的坡度i＝1∶0.25.为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i＝1∶1.75.施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备．工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？

    (参考数据：tan 31°≈0.60，sin 31°≈0.52)

    查看答案和解析>>

    同步练习册答案