
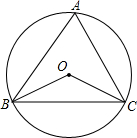
 如图.点O是△ABC的外心.∠A=72°.
如图.点O是△ABC的外心.∠A=72°.分析 (1)由圆周角定理即可得出结果;
(2)作OM⊥BC于M,则BM=CM=$\frac{1}{2}$BC=12cm,∠OMB=90°,∠BOM=$\frac{1}{2}$∠COB=72°,由三角函数求出OB即可.
解答 解:(1)∵点O是△ABC的外心.∠A=72°,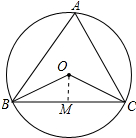 ∴∠COB=2∠A=144°;
∴∠COB=2∠A=144°;
(2)作OM⊥BC于M,如图所示:
则BM=CM=$\frac{1}{2}$BC=12cm,∠OMB=90°,∠BOM=$\frac{1}{2}$∠COB=72°,
∵sin∠BOM=$\frac{BM}{OB}$,
∴OB=$\frac{BM}{sin72°}$=$\frac{12}{0.9511}$≈12.6(cm),
即△ABC外接圆的半径为12.6cm.
点评 本题考查了三角形的外接圆于外心、圆周角定理、垂径定理、等腰三角形的性质、三角函数;熟练掌握圆周角定理和垂径定理,运用三角函数求出OB是解决(2)的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=$\frac{1}{2}$x2+2x-1的图象如图所示,利用该图象探索方程$\frac{1}{2}$x2+2x-1=0的正根的近似值(精确到0.1).
二次函数y=$\frac{1}{2}$x2+2x-1的图象如图所示,利用该图象探索方程$\frac{1}{2}$x2+2x-1=0的正根的近似值(精确到0.1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设ab≠0且b>a,
设ab≠0且b>a,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:| 操作次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com