
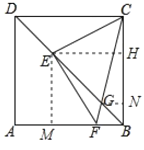
【题目】如图,在正方形 ABCD 中,AB=6,点 E 在对角线 BD 上,DE=![]() ,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
(1)求证:CE=EF;
(2)求 FB 的长;
(3)连接 FC 交 BD 于点 G.求 BG 的长.

【答案】(1)见解析(2)4(3)![]()
【解析】
(1)过E作EM⊥AB于M,EH⊥BC于H,根据正方形的性质得到∠EBM=∠HBE=45![]() ,求得EM=EH,根据全等三角形的性质即可得到结论;
,求得EM=EH,根据全等三角形的性质即可得到结论;
(2)根据勾股定理得到BD=6![]() ,得到AM=CH=1,根据全等三角形的性质得到FM=CH=1,于是得到结论;
,得到AM=CH=1,根据全等三角形的性质得到FM=CH=1,于是得到结论;
(3)过G作GN⊥BC于N,设GN=BN=x,根据相似三角形的性质即可得到结论.
(1)过E作EM⊥AB于M,EH⊥BC于H,
∵四边形ABCD是正方形,
∴∠EBM=∠HBE=45![]() ,
,
∴EM=EH,
∵∠EMB=∠MBH=∠BHE=90![]() ,
,
∴∠MEH=90![]() ,
,
∵EF⊥CE,
∴∠CEF=90![]() ,
,
∴∠MEF=∠CEH,
∴△EMF≌△EHC(ASA),
∴CE=EF;
(2)∵AB=6,
∴BD=6![]() ,
,
∵DE=![]() ,
,
∴BE=BDDE=5![]() ,
,
∵BM2+EM2=BE2,BM=EM
∴BM=BH=5,
∴AM=CH=1,
∵△EMF≌△EHC,
∴FM=CH=1,
∴BF=ABAMMF=611=4;
(3)过G作GN⊥BC于N,
∴GN=BN,
设GN=BN=x,
∴CN=6x,
∵GN⊥BC,AB⊥BC,
∴GN∥BF,
∴△CGN∽△CFB,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴BN=GN=![]() ,
,
∴BG=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.

查看答案和解析>>
科目:初中数学 来源: 题型:
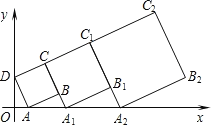
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2019个正方形的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和哥哥小明分别从家和图书馆同时出发,沿同一条路相向而行,小丽开始跑步,遇到哥哥后改为步行,到达图书馆恰好用35分钟,小明匀速骑自行车直接回家,骑行10分钟后遇到了妹妺,再继续骑行5分钟,到家两人距离家的路程y(m)与各自离开出发的时间x(min)之间的函数图象如图所示:
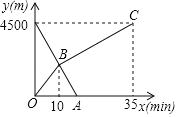
(1)求两人相遇时小明离家的距离;
(2)求小丽离距离图书馆500m时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
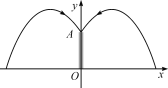
【题目】某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.
查看答案和解析>>
科目:初中数学 来源: 题型:
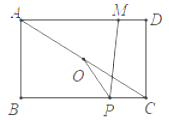
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测量斜坡![]() 旁一棵垂直于地面
旁一棵垂直于地面![]() 的树
的树![]() 的高度,他们先在点
的高度,他们先在点![]() 处测得树顶
处测得树顶![]() 的仰角为
的仰角为![]() ,然后在坡顶
,然后在坡顶![]() 测得树顶
测得树顶![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的长度为
的长度为![]() ,斜坡顶点
,斜坡顶点![]() 到地面的垂直高度
到地面的垂直高度![]() ,则树
,则树![]() 的高度是( )
的高度是( )![]()
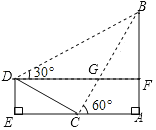
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商在今年1月份用2.2万元购进![]() 种水果和
种水果和![]() 种水果共400箱.其中
种水果共400箱.其中![]() 、
、![]() 两种水果的数量比为5:3.已知
两种水果的数量比为5:3.已知![]() 种水果的售价是
种水果的售价是![]() 种水果售价的2倍少10元,预计当月即可全部售完.
种水果售价的2倍少10元,预计当月即可全部售完.
(1)该水果商想通过本次销售至少盈利8000元,则每箱![]() 水果至少卖多少元?
水果至少卖多少元?
(2)若![]() 、
、![]() 两种水果在(1)的价格销售,但在实际销售中,受市场影响,
两种水果在(1)的价格销售,但在实际销售中,受市场影响,![]() 水果的销量还是下降了
水果的销量还是下降了![]() ,售价下降了
,售价下降了![]() ;
;![]() 水果的销量下降了
水果的销量下降了![]() ,但售价不变.结果
,但售价不变.结果![]() 、
、![]() 两种水果的销售总额相等.求
两种水果的销售总额相等.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
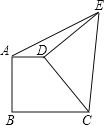
A. 1 B. 2 C. 3 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com