
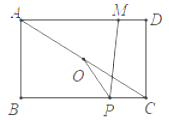
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
【答案】![]()
【解析】
连接MO并延长交BC于P,则此时,PMPO的值最大,且PMPO的最大值=OM,根据全等三角形的性质得到AM=CP=4,OM=OP,求得PB=1,过M作MN⊥BC于N,得到四边形MNCD是矩形,得到MN=CD,CN=DM,根据勾股定理即可得到结论.
∵在矩形ABCD中,AD=5,MD=1,
∴AM=AD﹣DM=5﹣1=4,
连接MO并延长交BC于P,
则此时,PM﹣PO的值最大,且PM﹣PO的最大值=OM,
∵AM∥CP,
∴∠MAO=∠PCO,
∵∠AOM=∠COP,AO=CO,
∴△AOM≌△COP(ASA),
∴AM=CP=4,OM=OP,
∴PB=5﹣4=1,
过M作MN⊥BC于N,
∴四边形MNCD是矩形,
∴MN=CD=AB=4,CN=DM=1,
∴PN=5﹣1﹣1=3,
∴MP=![]() ,
,
∴OM=![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】小颖在完成一项“社会调查”作业时,需要调查城市送餐人员的收入情况,他了解到劳务公司为了鼓励送餐员的工作积极性,实行“月总收入![]() 基本工资(固定)
基本工资(固定)![]() 送餐单数奖励”的方法计算薪资,调查中获得如下信息:
送餐单数奖励”的方法计算薪资,调查中获得如下信息:
送餐员 | 小李 | 小杨 |
月送餐单数/单 | 292 | 273 |
月总收入/元 | 3384 | 3346 |
送餐每单奖励![]() 元,送餐员月基本工资为
元,送餐员月基本工资为![]() 元;
元;
(1)求a、b的值;
(2)若月送餐单数超过300单时,超过部分每单的奖金增加1元.假设月送餐单数为![]() 单,月总收入为
单,月总收入为![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式,若送餐员小李计划月收入不低于5200元,那么他每月至少要送多少单?
的函数关系式,若送餐员小李计划月收入不低于5200元,那么他每月至少要送多少单?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
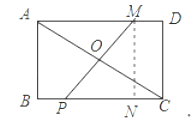
【题目】在矩形ABCD中作图:①分别以点B,C为圆心,BC长为半径画弧,分别交AD于点H,G;②分别以点B,C为圆心,大于BC的一半长为半径画弧,两弧相交于点E,F;③作直线EF,交AD于点P.下列结论不一定成立的是( )

A.BC=BHB.CG=AD
C.PB=PCD.GH=2AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,AB=6,点 E 在对角线 BD 上,DE=![]() ,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
,连接 CE,过点 E作 EF⊥CE,交线段 AB 于点 F
(1)求证:CE=EF;
(2)求 FB 的长;
(3)连接 FC 交 BD 于点 G.求 BG 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
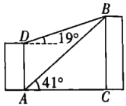
【题目】如图,已知一居民楼![]() 前方
前方![]() 处有一建筑物
处有一建筑物![]() ,小敏在居民楼的顶部
,小敏在居民楼的顶部![]() 处和底部
处和底部![]() 处分别测得建筑物顶部
处分别测得建筑物顶部![]() 的仰角为
的仰角为![]() 和
和![]() ,求居民楼的高度
,求居民楼的高度![]() 和建筑物的高度
和建筑物的高度![]() (结果取整数).
(结果取整数).
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
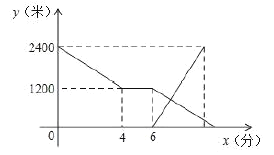
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程![]() (米)与小张出发后的时间
(米)与小张出发后的时间![]() (分)之间的函数图象如图所示.
(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时![]() 与
与![]() 之间的函数表达式:.
之间的函数表达式:.
(3)求小张与小李相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
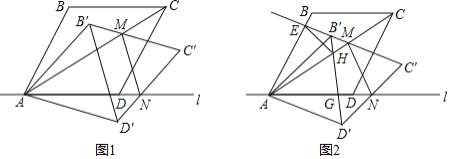
【题目】图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.
(1)当MN∥B′D′时,求α的大小.
(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com