
已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
考点: 待定系数法求二次函数解析式;二次函数图象上点的坐标特征.
分析: (1)已知了二次函数图象上的三点坐标,即可用待定系数法求出抛物线的解析式;
(2)将P点坐标代入二次函数的解析式中进行验证,即可得到P点是否在此函数图象上的结论;
令抛物线解析式的y=0,即可求得抛物线与x轴交点A、B的坐标,也就得到了AB的长;以AB为底,P点纵坐标的绝对值为高即可求得△PAB的面积.
解答: 解:(1)设二次函数的解析式为y=ax2+bx+c;
∵二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),则有:
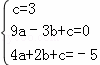 ,
,
解得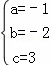 ;
;
∴y=﹣x2﹣2x+3.
(2)∵﹣(﹣2)2﹣2×(﹣2)+3=﹣4+4+3=3,
∴点P(﹣2,3)在这个二次函数的图象上,
∵﹣x2﹣2x+3=0,
∴x1=﹣3,x2=1;
∴与x轴的交点为:(﹣3,0),(1,0),
∴S△PAB=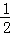 ×4×3=6.
×4×3=6.
点评: 此题主要考查了二次函数解析式的确定及图形面积的求法.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
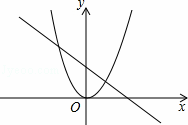
已知函数y1=x2与函数y2= 的图象大致如图.若y1<y2,则自变量x的取值范围是( )
的图象大致如图.若y1<y2,则自变量x的取值范围是( )
A. 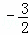 <x<2 B. x>2或x<
<x<2 B. x>2或x<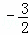 C. ﹣2<x<
C. ﹣2<x<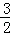 D. x<﹣2或x>
D. x<﹣2或x>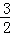
查看答案和解析>>
科目:初中数学 来源: 题型:
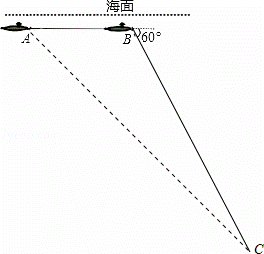
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: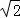 ≈1.414,
≈1.414,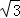 ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com