
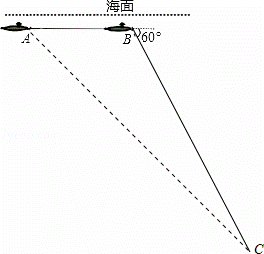
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: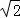 ≈1.414,
≈1.414,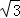 ≈1.732)
≈1.732)
考点: 解直角三角形的应用-仰角俯角问题.
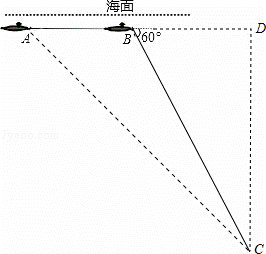
分析: (1)过点C作CD垂直AB延长线于点D,设CD为x米,在Rt△ACD和Rt△BCD中,分别表示出AD和BD的长度,然后根据AB=2000米,求出x的值,求出点C距离海面的距离,判断是否在极限范围内;
(2)根据时间=路程÷速度,求出时间即可.
解答: 解:(1)过点C作CD垂直AB延长线于点D,
设CD=x米,
在Rt△ACD中,
∵∠DAC=45°,
∴AD=x,
在Rt△BCD中,
∵∠CBD=60°,
∴BD= x,
x,
∴AB=AD﹣BD=x﹣ x=2000,
x=2000,
解得:x≈4732,
∴船C距离海平面为4732+1800=6532米<7062.68米,
∴沉船C在“蛟龙”号深潜极限范围内;
(2)t=1800÷2000=0.9(小时).
答:“蛟龙”号从B处上浮回到海面的时间为0.9小时.
点评: 本题考查了解直角三角形的应用,解答本题的关键是利用俯角构造直角三角形,利用三角函数的知识求解,难度一般.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在平面直角坐标系xOy中,抛物线m:y=﹣2x2﹣2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在轴y上,则下列各点的坐标不正确的是( )
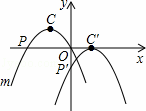
A. C(﹣ ,
, ) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣
) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣ )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
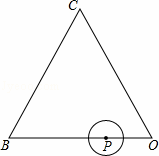
如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为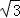 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
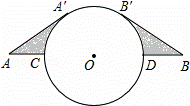
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+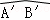 +BB′为最短路线(其中AA′,BB′都与⊙O相切).
+BB′为最短路线(其中AA′,BB′都与⊙O相切).
(1)你能计算出这段公路的长度吗?(结果精确到0.1km)
(2)阴影部分的面积是多少?(结果精确到1km2)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
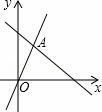
A. x<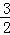 B. x<3 C. x>
B. x<3 C. x>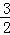 D. x>3
D. x>3
查看答案和解析>>
科目:初中数学 来源: 题型:
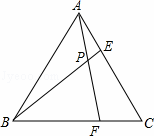
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P;
(1)如AE=CF=2,
①试判断AF与BE的数量关系,并说明你的理由;
②试求AP•AF的值;
(2)若AF=BE,当点E从A运动到点C时,请直接写出点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:
| 班级 | 参加人数 | 平均字数 | 中位数 | 方差 |
| 甲 | 55 | 135 | 149 | 191 |
| 乙 | 55 | 135 | 151 | 110 |
有一位同学根据上面表格得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是 (填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com