
如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为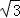 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
6 2
考点: 直线与圆的位置关系;轨迹.
分析: 当点P在OB上且与边OC相切时,作PH⊥OC于H,根据直线与圆相切的判定得到PH=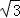 ,再根据等边三角形的性质得∠O=60°,在Rt△OPH中,利用含30度的直角三角形三边的关系得到OH=
,再根据等边三角形的性质得∠O=60°,在Rt△OPH中,利用含30度的直角三角形三边的关系得到OH=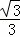 PH=1,OP=2OH=2,即点P在OB,OP=2时,⊙P与边OC相切,然后利用同样的方法可得BP=2或CP=2时,⊙P与△OBC的边相切.
PH=1,OP=2OH=2,即点P在OB,OP=2时,⊙P与边OC相切,然后利用同样的方法可得BP=2或CP=2时,⊙P与△OBC的边相切.
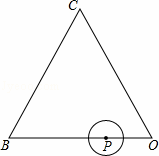
解答: 解:当点P在OB上且与边OC相切时,如图所示:
作PH⊥OC于H,则PH=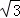 ,
,
∵△OBC为等边三角形,
∴∠O=60°,
在Rt△OPH中,OH=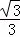 PH=1,
PH=1,
OP=2OH=2,
∴点P在OB,OP=2时,⊙P与边OC相切,
同理可得点P在OB,BP=2时,⊙P与边BC相切;
点P在BC,BP=2时,⊙P与边OB相切,
点P在BC,CP=2时,⊙P与边OC相切,
点P在OC,CP=2时,⊙P与边BC相切,
点P在OC,OP=2时,⊙P与边OB相切,
综上所述,⊙P运动一圈与△OBC的边相切6次,每次相切时,点P分别距离△OBC的顶点2个单位;
故答案为:6;2.

点评: 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.直线l和⊙O相交⇔d<r;直线l和⊙O相切⇔d=r;直线l和⊙O相离⇔d>r.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:
根据下面表格中的对应值:
x 3.24 3.25 3.26
ax2+bx+c ﹣0.02 0.01 0.03
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
A. x<3.24 B. 3.24<x<3.25 C. 3.25<x<3.26 D. x>3.26
查看答案和解析>>
科目:初中数学 来源: 题型:
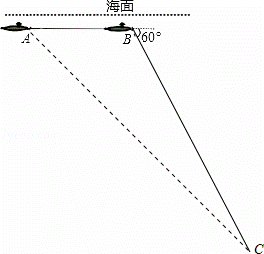
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: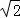 ≈1.414,
≈1.414,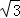 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线y=﹣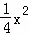 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
(1)求抛物线的解析式及其对称轴方程.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D的坐标和△DBC的面积;若不存在,请说明理由.
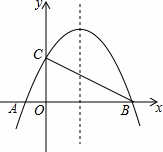
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D为CB边上一动点,CD= BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.
BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.
(1)若n=3,则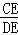 = ,
= ,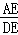 = ;
= ;
(2)若n=2,求证:AF=2FC;
(3)若F为AC的中点,请直接写出n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com