
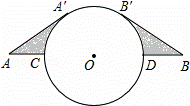
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+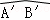 +BB′为最短路线(其中AA′,BB′都与⊙O相切).
+BB′为最短路线(其中AA′,BB′都与⊙O相切).
(1)你能计算出这段公路的长度吗?(结果精确到0.1km)
(2)阴影部分的面积是多少?(结果精确到1km2)
考点: 扇形面积的计算;弧长的计算.
专题: 应用题.
分析: (1)连结OA′、OB′,如图,根据切线的性质得OA′⊥AA′,OB′⊥BB′,再计算出OA=OB=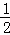 AB=20,在Rt△OAA′中,利用正弦的定义可求出∠A=30°,则∠AOA′=60°,AA′=
AB=20,在Rt△OAA′中,利用正弦的定义可求出∠A=30°,则∠AOA′=60°,AA′= OA′=10
OA′=10 ,同理可得∠BOB′=60°,BB′=10
,同理可得∠BOB′=60°,BB′=10 ,于是∠A′OB′=60°,接着根据弧长公式计算出弧A′B′的长度,然后求AA′+
,于是∠A′OB′=60°,接着根据弧长公式计算出弧A′B′的长度,然后求AA′+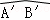 +BB′的值即可;
+BB′的值即可;
(2)用△AA′O与△BB′O的面积减去扇形A′OC和扇形B′OD的面积即可.
解答: 解:(1)连结OA′、OB′,如图,
∵AA′,BB′都与⊙O相切,
∴OA′⊥AA′,OB′⊥BB′,
∵点O为AB的中点,
∴OA=OB=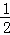 AB=20,
AB=20,
而OA′=OB′=10,
在Rt△OAA′中,∵sin∠A= =
=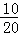 =
=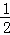 ,
,
∴∠A=30°,
∴∠AOA′=60°,AA′=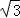 OA′=10
OA′=10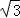 ,
,
同理可得∠BOB′=60°,BB′=10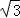 ,
,
∴∠A′OB′=60°,
∴弧A′B′的长度=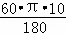 =
=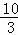 π,
π,
∴这段公路的长度=10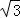 +
+ π+10
π+10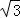 ≈45.1(km);
≈45.1(km);
(2)S△AA′O= •sin∠A=
•sin∠A=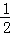 ×10
×10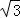 ×20×
×20×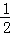 =50
=50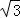 ,
,
S△B′OB=S△AA′O=50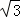 ,
,
S扇形A′OC=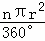 =
= =
=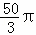 ,同理可得,S扇形B′OB=
,同理可得,S扇形B′OB=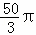 ,
,
所以S阴影=S△AA′O+S△B′OB﹣S扇形A′OC ﹣S扇形B′OB=2×50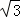 ﹣2×
﹣2×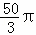 =100
=100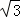
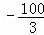 π=277.9(km2).
π=277.9(km2).

点评: 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了弧长公式,扇形的面积公式,作出适当的辅助线是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
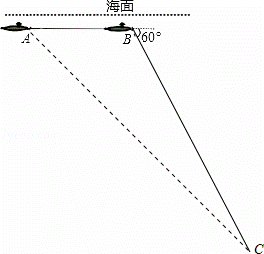
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: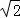 ≈1.414,
≈1.414,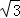 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形纸片ABCD中,AB=3,AD=5.折叠纸片,使点A落在BC边上的A′处,
折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动。若限定点P,Q
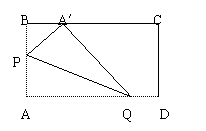 分别在AB,AD边上移动,则点A′在BC边上可
分别在AB,AD边上移动,则点A′在BC边上可 移动的最大距离为( )
移动的最大距离为( )
A、2 B、4
C、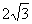 D、
D、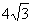
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别求出以上三组数据的平均数、众数、中位数.
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的 特征数.
(3)如果你是顾客,会选购哪家工厂的产品?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com