
����Ŀ����ͼ���Գ���Ϊֱ��x= ![]() �������߾�����A��6��0����B��0��4����
�������߾�����A��6��0����B��0��4����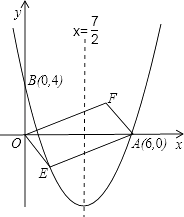
��1���������߽���ʽ���������ꣻ
��2�����E��x��y������������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ���ƽ���ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�ٵ�ƽ���ı���OEAF�����Ϊ24ʱ�����ж�ƽ���ı���OEAF�Ƿ�Ϊ���Σ�
���Ƿ���ڵ�E��ʹƽ���ı���OEAFΪ�����Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��Ϊ�����ߵĶԳ�����x= ![]() ��
��
�����ʽΪy=a��x�� ![]() ��2+k��
��2+k��
��A��B�������������ʽ���� 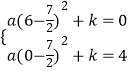 ��
��
���a= ![]() ��k=��
��k=�� ![]() ��
��
�������߽���ʽΪy= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��������
�������� ![]() ����
���� ![]() ��
��
��2��
�⣺�ߵ�E��x��y�����������ϣ�λ�ڵ������ޣ��������ʺ�y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��y��0��
����y��0����y��ʾ��E��OA�ľ��룮
��OA��OEAF�ĶԽ��ߣ�
��S=2S��OAE=2�� ![]() ��OA|y|=��6y=��4��x��
��OA|y|=��6y=��4��x�� ![]() ��2+25��
��2+25��
��Ϊ��������x������������ǣ�1��0���ͣ�6��0����
�����Ա���x��ȡֵ��Χ��1��x��6��
�� �������⣬��S=24ʱ������4��x�� ![]() ��2+25=24��
��2+25=24��
���ã�x�� ![]() ��2=
��2= ![]() ��
��
���x1=3��x2=4��
������ĵ�E��������
�ֱ�ΪE1��3����4����E2��4����4����
��E1��3����4������OE=AE��
����ƽ���ı���OEAF�����Σ�
��E2��4����4��������OE=AE��
����ƽ���ı���OEAF�������Σ�
�ڵ�OA��EF����OA=EFʱ��ƽ���ı���OEAF�������Σ�
��ʱ��E������ֻ���ǣ�3����3����
������Ϊ��3����3���ĵ㲻���������ϣ�
�ʲ����������ĵ�E��ʹƽ���ı���OEAFΪ������
����������1����֪�������ߵĶԳ������ʽ�����ö���ʽ���κ���ͨʽ���������ߣ�Ȼ��A��B�������������⼴�ɣ���2��ƽ���ı��ε����Ϊ������OEA�����2������˿ɸ���E��ĺ����꣬�������ߵĽ���ʽ���E��������꣬��ôE��������ľ���ֵ��Ϊ��OAE�ĸߣ��ɴ˿ɸ��������ε������ʽ�ó���AOE�������x�ĺ�����ϵʽ�����ɵó�S��x�ĺ�����ϵʽ��
�ٽ�S=24����S��x�ĺ�����ϵʽ�����x��ֵ�����ɵó�E��������OE��OA�ij������ƽ���ı���OEAF�����Σ���������ƽ���ı����������ߵij���ȣ��ݴ˿��жϳ��ı���OEAF�Ƿ�Ϊ���Σ�
������ı���OEAF�������Σ���ô������OEAӦ���ǵ���ֱ�������Σ���E�������Ϊ��3����3��������������ߵĽ���ʽ�м����жϳ��Ƿ���ڷ���������E�㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4�µ�ij��С���ڡ�A���С����ˡ�ȸ���ɿ������͡�Ȥ���С���ɡ���10������֪��ȸ���ɿ�����ÿ��22Ԫ����Ȥ���С���ɡ�ÿ��2Ԫ���ܹ�������80Ԫ��
��1�������С������βɹ��У���ȸ���ɿ������͡�Ȥ���С���ɡ������˶��ٰ���
��2������һ���ڼ䣬С�����֣�A��B��������ͬ���ļ۸����ͬ������Ʒ�������ָ����Ƴ���ͬ���Żݷ�������A�����ۼƹ��ﳬ��50Ԫ����50Ԫ�IJ��ִ���ۣ���B�����ۼƹ��ﳬ��100Ԫ����100Ԫ�IJ��ִ���ۣ� �����ʡ���һ���ڼ䣬��С���������100Ԫ��ȥ�ļҳ��й�������㣿
�ڡ���һ���ڼ䣬С���ֵ���B���С�������һЩ��ȸ���ɿ����������������ٹ�����ٰ�ʱ��ƽ��ÿ���۸���20Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijСѧ���꼶�����꼶��ȫ��ѧ���μӡ����ǡ�֪ʶ���ԣ������10�⣬ÿ��10�֣����������ȡ�˲���ѧ���ijɼ�����ͳ�ƣ����ֳ���ѧ��ÿ�����ٴ����6�⣬�ֽ��й�������������Ƴ����¡��꼶����ͳ��ͼ������δȫ����ɵġ��ɼ����ͳ�Ʊ�����
�ɼ����ͳ�Ʊ�
�ɼ� | 100�� | 90�� | 80�� | 70�� | 60�� |
���� | 21 | 40 | 5 | ||
Ƶ�� | 0.3 |
����ͼ�����ṩ����Ϣ���ش��������⣺
��1���뽫ͳ�Ʊ���������
�ɼ����ͳ�Ʊ�
�ɼ� | 100�� | 90�� | 80�� | 70�� | 60�� |
���� | 21 | 40 | 5 | ||
Ƶ�� | 0.3 |
��2������ѧ���У��ɼ�Ϊ80�ֵ�ѧ�������� ���������� �֣���λ���� �֣�
��3������Сѧ���꼶�����꼶����1800��ѧ������ɹ��Ƴ��ɼ�Ϊ70�ֵ�ѧ������Լ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ�����ڼ䣬ij�̳�Ϊ�������˿������ѣ��������ͼ��ʾ��һ��ת�̣�ת��ƽ���ֳ�3��. 
��1����ת����ת��һ�����õ���ɫ�ǻ�ɫ�ĸ��ʣ�
��2�������б�������״ͼ�ķ�����˵��ת����ת�����Σ��������õ���ɫ��ͬ�ĸ���.
��3�����̳�������������ֽ�������������һ��ת����ת��һ�Σ���ת�õ���ɫ�ǻ�ɫ��ɵý�����������ת����ת�����Σ�������ת�õ���ɫ��ͬ��ɵý���������ǹ˿ͣ���ѡ�����ַ����Ƚϻ��㣿Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ4��������ABCD�ڽ��ڵ�O����E�� ![]() �ϵ�һ���㣨����A��B�غϣ�����F��
�ϵ�һ���㣨����A��B�غϣ�����F�� ![]() �ϵ�һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��H���ҡ�EOF=90�㣬�����½��ۣ�������ȷ�ĸ����ǣ� ��. ��
�ϵ�һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��H���ҡ�EOF=90�㣬�����½��ۣ�������ȷ�ĸ����ǣ� ��. �� ![]() =
= ![]() �� �ڡ�OGH�ǵ��������Σ� ���ı���OGBH��������ŵ�Eλ�õı仯���仯���ܡ�GBH�ܳ�����СֵΪ4+
�� �ڡ�OGH�ǵ��������Σ� ���ı���OGBH��������ŵ�Eλ�õı仯���仯���ܡ�GBH�ܳ�����СֵΪ4+ ![]() .
.
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��ֱ��AB����A����4����4����B��0��4�����㣬ֱ��AC��y=�� ![]() x��6��y���ڵ�C����E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G��
x��6��y���ڵ�C����E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G��
��1����������y=��x2+bx+c�ı���ʽ��
��2������GB��EO�����ı���GEOB��ƽ���ı���ʱ�����G�����ꣻ
��3������y���ϴ���һ��H������EH��HF������E�˶���ʲôλ��ʱ����A��E��F��HΪ������ı����Ǿ��Σ������ʱ��E��H�����ꣻ
���ڢٵ�ǰ���£��Ե�EΪԲ�ģ�EH��Ϊ�뾶��Բ����MΪ��E��һ���㣬�� ![]() AM+CM������Сֵ��
AM+CM������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ����ƽ��ֱ������ϵxoy�У��ı���OABC�Ǿ��Σ�OA=4��OC=3������P�ӵ�C������������CB������ÿ��2����λ���ȵ��ٶ��˶���ͬʱ������Q�ӵ�O��������x�������᷽����ÿ��1����λ���ȵ��ٶ��˶������P����Q���˶�ʱ��Ϊt��s����
��1����t=1sʱ������O��P��A����������ߵĽ���ʽ��
��2����t=2sʱ����tan��QPA��ֵ��
��3�����߶�PQ���߶�AB�ཻ�ڵ�M����BM=2AMʱ����t��s����ֵ��
��4������CQ������P��Q���˶������У��ǡ�CQP�����OABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com