
【题目】如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣ ![]() x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 ![]() AM+CM它的最小值.
AM+CM它的最小值.
【答案】
(1)
解:∵点A(﹣4,﹣4),B(0,4)在抛物线y=﹣x2+bx+c上,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+4;
(2)
解:设直线AB的解析式为y=kx+n过点A,B,
∴ ![]() ,
,
∴ ![]() ,
,
∴直线AB的解析式为y=2x+4,
设E(m,2m+4),
∴G(m,﹣m2﹣2m+4),
∵四边形GEOB是平行四边形,
∴EG=OB=4,
∴﹣m2﹣2m+4﹣2m﹣4=4,
∴m=﹣2,
∴G(﹣2,4);
(3)
解:①如图1,
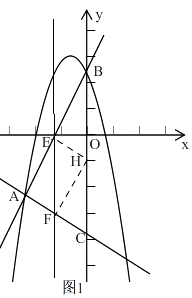
由(2)知,直线AB的解析式为y=2x+4,
∴设E(a,2a+4),
∵直线AC:y=﹣ ![]() x﹣6,
x﹣6,
∴F(a,﹣ ![]() a﹣6),
a﹣6),
设H(0,p),
∵以点A,E,F,H为顶点的四边形是矩形,
∵直线AB的解析式为y=2x+4,直线AC:y=﹣ ![]() x﹣6,
x﹣6,
∴AB⊥AC,
∴EF为对角线,
∴ ![]() (﹣4+0)=
(﹣4+0)= ![]() (a+a),
(a+a), ![]() (﹣4+p)=
(﹣4+p)= ![]() (2a+4﹣
(2a+4﹣ ![]() a﹣6),
a﹣6),
∴a=﹣2,P=﹣1,
∴E(﹣2,0).H(0,﹣1);
②如图2,
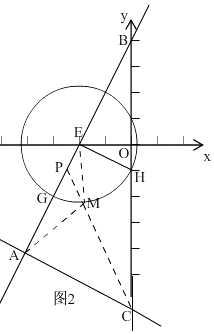
由①知,E(﹣2,0),H(0,﹣1),A(﹣4,﹣4),
∴EH= ![]() ,AE=2
,AE=2 ![]() ,
,
设AE交⊙E于G,取EG的中点P,
∴PE= ![]() ,
,
连接PC交⊙E于M,连接EM,
∴EM=EH= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠PEM=∠MEA,
,∵∠PEM=∠MEA,
∴△PEM∽△MEA,
∴ ![]() ,
,
∴PM= ![]() AM,
AM,
∴ ![]() AM+CM的最小值=PC,
AM+CM的最小值=PC,
设点P(p,2p+4),
∵E(﹣2,0),
∴PE2=(p+2)2+(2p+4)2=5(p+2)2,
∵PE= ![]() ,
,
∴5(p+2)2= ![]() ,
,
∴p=﹣ ![]() 或p=﹣
或p=﹣ ![]() (由于E(﹣2,0),所以舍去),
(由于E(﹣2,0),所以舍去),
∴P(﹣ ![]() ,﹣1),
,﹣1),
∵C(0,﹣6),
∴PC= ![]() =
= ![]() ,
,
即: ![]() AM+CM=
AM+CM= ![]() .
.
【解析】(1)利用待定系数法求出抛物线解析式;(2)先利用待定系数法求出直线AB的解析式,进而利用平行四边形的对边相等建立方程求解即可;(3)①先判断出要以点A,E,F,H为顶点的四边形是矩形,只有EF为对角线,利用中点坐标公式建立方程即可;②先取EG的中点P进而判断出△PEM∽△MEA即可得出PM= ![]() AM,连接CP交圆E于M,再求出点P的坐标即可得出结论.
AM,连接CP交圆E于M,再求出点P的坐标即可得出结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6. 
(1)实践操作:尺规作图,不写作法,保留作图痕迹. ①作∠ABC的角平分线交AC于点D.
②作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE、DF.
(2)推理计算:四边形BFDE的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x= ![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).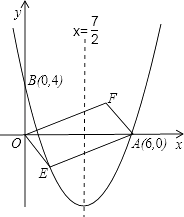
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的 ![]() O与边AB相交于点D,DE⊥AC,垂足为点E.
O与边AB相交于点D,DE⊥AC,垂足为点E. 
(1)求证:点D是AB的中点;
(2)判断DE与 ![]() O的位置关系,并证明你的结论;
O的位置关系,并证明你的结论;
(3)若 ![]() O的直径为3,cosB=
O的直径为3,cosB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P
求作:直线l的垂线,使它经过点P.
作法:如图:⑴在直线l上任取两点A、B;
⑵分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
⑶作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的跳水运动员人数为 , 图①中m的值为;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ![]() ,∠AEO=120°,则FC的长度为( )
,∠AEO=120°,则FC的长度为( ) 
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2 , 已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题: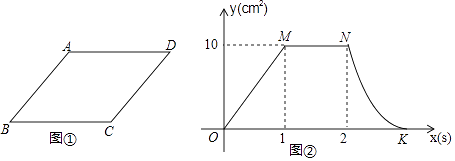
(1)当1<x<2时,△BPQ的面积(填“变”或“不变”);
(2)分别求出线段OM,曲线NK所对应的函数表达式;
(3)当x为何值时,△BPQ的面积是5cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平行四边形ABCD中,∠ABD=30°,AB=4,AE⊥BD,CF⊥BD,且,E,F恰好是BD的三等分点,又M、N分别是AB,CD的中点,那么四边形MENF的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com