
【题目】我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢? 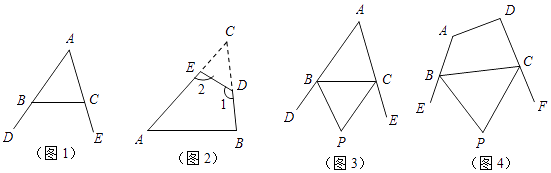
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案 .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
【答案】
(1)解:∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)50°
(3)∠P=90°﹣ ![]() ∠A
∠A
(4)解:延长BA、CD于Q,
则∠P=90°﹣ ![]() ∠Q,
∠Q,
∴∠Q=180°﹣2∠P,
∴∠BAD+∠CDA=180°+∠Q,
=180°+180°﹣2∠P,
=360°﹣2∠P.
【解析】(2)∵∠1+∠2=∠180°+∠C, ∴130°+∠2=180°+∠C,
∴∠C=50°;
3)∠DBC+∠ECB=180°+∠A,
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC+∠PCB= ![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)= ![]() (180°+∠A),
(180°+∠A),
在△PBC中,∠P=180°﹣ ![]() (180°+∠A)=90°﹣
(180°+∠A)=90°﹣ ![]() ∠A;
∠A;
即∠P=90°﹣ ![]() ∠A;
∠A;
所以答案是:50°,∠P=90°﹣ ![]() ∠A;
∠A;
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对三角形的外角的理解,了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明; 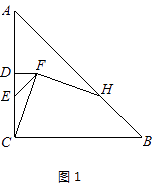
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明. 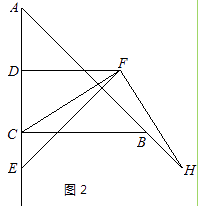
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)九年级(1)班共有 名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是 ;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论. 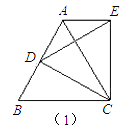
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由. 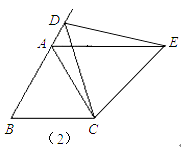
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:如图,已知在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上由B点向C点运动,同时,点Q在线段CA上由点C向点A运动. 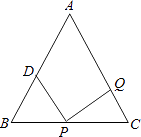
(1)如果点P、Q的速度均为3厘米/秒,经过1秒后,△BPD与△CQP是否全等?请说明理由;
(2)若点P的运动速度为2厘米/秒,点Q的运动速度为2.5厘米/秒,是否存在某一个时刻,使得△BPD与△CQP全等?如果存在请求出这一时刻并证明;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
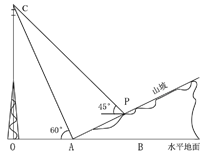
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为![]() (tan∠PAB=
(tan∠PAB=![]() )且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
)且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com