
【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
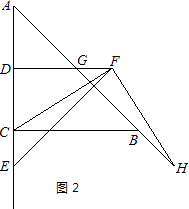
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明; 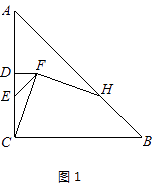
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明. 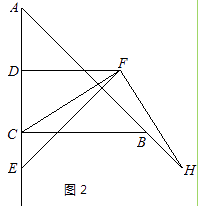
【答案】
(1)解:FH与FC的数量关系是:FH=FC.
证明如下:延长DF交AB于点G,
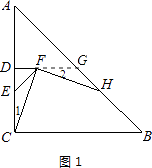
由题意,知∠EDF=∠ACB=90°,DE=DF,
∴DG∥CB,
∵点D为AC的中点,
∴点G为AB的中点,且 ![]() ,
,
∴DG为△ABC的中位线,
∴ ![]() .
.
∵AC=BC,
∴DC=DG,
∴DC﹣DE=DG﹣DF,
即EC=FG.
∵∠EDF=90°,FH⊥FC,
∴∠1+∠CFD=90°,∠2+∠CFD=90°,
∴∠1=∠2.
∵△DEF与△ADG都是等腰直角三角形,
∴∠DEF=∠DGA=45°,
∴∠CEF=∠FGH=135°,
∴△CEF≌△FGH,
∴CF=FH
(2)解:FH与FC仍然相等.
理由:由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG= ![]() BC,DC=
BC,DC= ![]() AC,
AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中
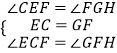 ,
,
∴△FCE≌△HFG(ASA),
∴HF=FC
【解析】(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠1=∠2=90°﹣∠DFC,∠CEF=∠FGH=135°,由AAS证出△CEF≌△FGH.∴CF=FH.(2)通过证明△CEF≌△FGH(ASA)得出.


科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,E是线段AB上一动点,点F在AD的延长线上运动,且DF=BE.
(1)求证:CE=CF.
(2)当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.
(3)若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例计算总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(1)笔试成绩的平均数是 ;
(2)写出说课成绩的中位数为 ,众数为 ;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你通过计算判断哪两位选手将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC中,AB、AC边的中垂线交于点O 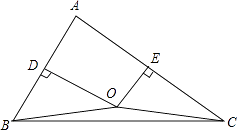
(1)若∠A=α(0°<α<90°),求∠BOC;
(2)试判断∠ABO+∠ACB是否为定值;若是,求出定值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢? 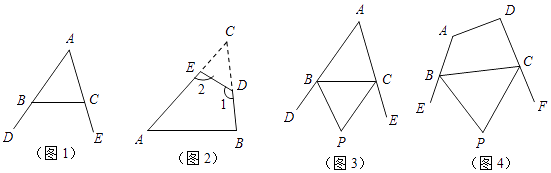
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案 .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com