
【题目】如图①,在正方形ABCD中,E是线段AB上一动点,点F在AD的延长线上运动,且DF=BE.
(1)求证:CE=CF.
(2)当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.
(3)若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?
【答案】
(1)
解:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF,
∴CE=CF
(2)
解:EG=BE+GD
理由:由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG,
∴GE=GF
∴GE=GF=DF+GD=BE+GD
(3)
解:如图,
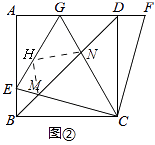
在GE上取一点H,使GH=GD,
∵△GCE≌△GCF,
∴∠DGN=∠HGN,∠F=∠GEC,
∵GN=GN,
∴△DGN≌△HGN,
∴DN=HN,
∴∠GDN=∠GHN=45°,
∵GE=GF,GD=GH,BE=DF,
∴DF=BE=EH,
∵∠F=∠GEC=∠BEC,∠EM=EM,
∴△BEM≌△HEM,
∴BM=HM,∠EBM=∠EHM=45°,
∴∠NHM=90°
∴线段BM、MN、DN为三边构成的是一个直角三角形
【解析】(1)由条件直接证明三角形全等就可以得出CE=CF.(2)由条件和(1)的结论可以证明三角形ECG全等三角形FCG,可以得出EG=FG,可以得出GE=BE+GD.(3)先判断出△DGN≌△HGN得到结论,再判断出△BEM≌△HEM,最后简单计算即可.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假如某市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费. 小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:
(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘坐出租车从汽车站到市政府走了10千米,应付车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( ) 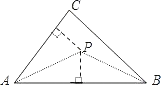
A.P是∠A与∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为A
D.AB两边上的高的交点
E.P为A
F.AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请用“<”或“>”连接下面的式子.
(1)4______-6 (2)-8______-3
(3)-4.5_______-4 (4)7+(-3)_________4+(-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明; 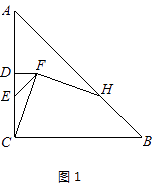
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明. 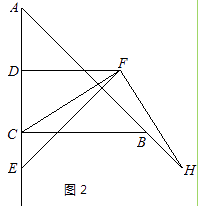
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com