
【题目】附加题:如图,已知在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上由B点向C点运动,同时,点Q在线段CA上由点C向点A运动. 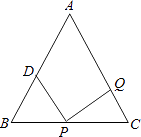
(1)如果点P、Q的速度均为3厘米/秒,经过1秒后,△BPD与△CQP是否全等?请说明理由;
(2)若点P的运动速度为2厘米/秒,点Q的运动速度为2.5厘米/秒,是否存在某一个时刻,使得△BPD与△CQP全等?如果存在请求出这一时刻并证明;如果不存在,请说明理由.
【答案】
(1)解:△BPD与△CQP是全等,
理由是:当t=1秒时BP=CQ=3,
CP=8﹣3=5,
∵D为AB中点,
∴BD= ![]() AC=5=CP,
AC=5=CP,
∵AB=AC,
∴∠B=∠C,
在△BDP和△CPQ中
∵ 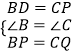 ,
,
∴△BDP≌△CPQ(SAS)
(2)解:假设存在时间t秒,使△BDP和△CPQ全等,
则BP=2t,BD=5,CP=8﹣2t,CQ=2.5t,
∵△BDP和△CPQ全等,∠B=∠C,
∴ ![]() 或
或 ![]() (此方程组无解),
(此方程组无解),
解得:t=2,
∴存在时刻t=2秒时,△BDP和△CPQ全等,
此时BP=4,BD=5,CP=8﹣4=4=BP,CQ=5=BD,
在△BDP和△CQP中
∵  ,
,
∴△BDP≌△CQP(SAS).
【解析】(1)求出BP=CQ,CP=BD,∠B=∠C,根据SAS证出两三角形全等即可;(2)假设存在时刻t,根据全等三角形的性质得出方程组,求出t后,看看是否符合题意,再根据全等三角形的判定推出即可.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC中,AB、AC边的中垂线交于点O 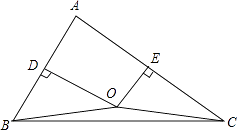
(1)若∠A=α(0°<α<90°),求∠BOC;
(2)试判断∠ABO+∠ACB是否为定值;若是,求出定值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列三角形不一定全等的是( )
A.面积相等的两个三角形
B.周长相等的两个等边三角形
C.斜边和一条直角边分别对应相等的两个直角三角形
D.有一个角是100°,腰长相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)20﹣22+(﹣3)3+( ![]() )﹣1
)﹣1
(2)(﹣3a3)3a3+(2a3)4﹣(﹣2a6)2
(3)(x+y)2(x﹣y)2
(4)982(用乘法公式计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢? 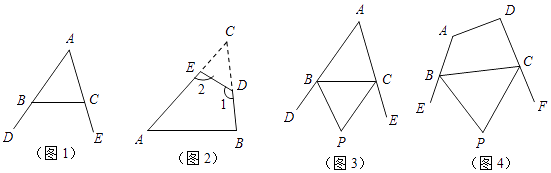
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案 .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com