
【题目】解答
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论. 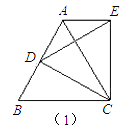
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由. 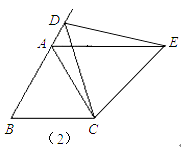
【答案】
(1)解:结论:AC=AD+AE,
证明如下:
∵△ABC、△CDE为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ECA+∠ACD=∠ACD+∠BCD,
∴∠ECA=∠BCD,
在△ACE和△BCD中
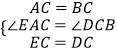
∴△ACE≌△BCD(SAS),
∴AE=BD,
∴AC=AB=AD+BD=AD+AE
(2)解:结论:AC=AE﹣AD,
理由如下:
同(1)可证明△ACE≌△BCD,
∴AE=BD,
∴AC=AB=BD﹣AD=AE﹣AD
【解析】(1)利用条件可证明△ACE≌△BCD,则可得到AE=BE,再利用线段的和差可证得结论AC=AD+AE;(2)由条件可证明△ACE≌△BCD,同样可以得到结论AC=AE﹣AD.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例计算总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(1)笔试成绩的平均数是 ;
(2)写出说课成绩的中位数为 ,众数为 ;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你通过计算判断哪两位选手将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)20﹣22+(﹣3)3+( ![]() )﹣1
)﹣1
(2)(﹣3a3)3a3+(2a3)4﹣(﹣2a6)2
(3)(x+y)2(x﹣y)2
(4)982(用乘法公式计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC. 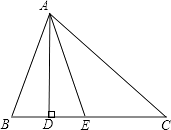
(1)已知∠B=60°,∠B=30°,求∠DAE的度数;
(2)已知∠B=3∠C,说明:∠DAE=∠C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢? 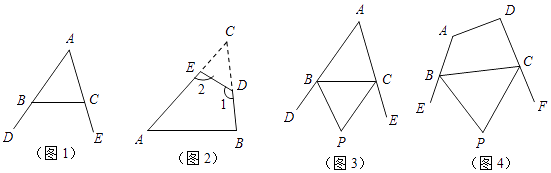
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案 .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s). 
(1)当t为何值时,△ABQ≌△CBP.
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com