
【题目】如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC. 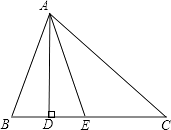
(1)已知∠B=60°,∠B=30°,求∠DAE的度数;
(2)已知∠B=3∠C,说明:∠DAE=∠C.
【答案】
(1)解:∵∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣30°=90°,
又∵AE平分∠BAC,
∴∠BAE= ![]() ∠BAC=45°.
∠BAC=45°.
∵直角△ABD中,∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°;
(2)解:设∠C=x,则∠B=3x∴∠BAC=180°﹣4x
∵AE平分∠BAC,
∴∠BAE=90﹣2x,
∵AD⊥BC,
∴∠BAD=90﹣3x,
∴∠DAE=∠BAE﹣∠BAD=(90﹣2x)﹣(90﹣3x)=x,
∴∠DAE=∠C.
【解析】(1)首先利用三角形内角和定理求得∠BAC的度数,则∠BAE即可求得,然后在直角△ABD中求得∠BAD的度数,根据∠DAE=∠BAE﹣∠BAD求解;(2)设∠C=x,则∠B=3x,利用(1)的思路表示出∠DAE即可证得.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数为( )
①过一点有无数条直线与已知直线平行; ②如果a∥b,a∥c,那么b∥c;
③如果两线段不相交,那么它们就平行; ④如果两直线不相交,那么它们就平行.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论. 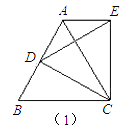
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由. 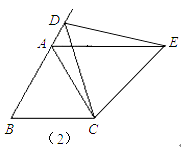
查看答案和解析>>
科目:初中数学 来源: 题型:
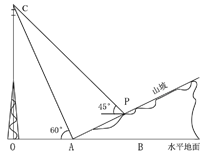
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为![]() (tan∠PAB=
(tan∠PAB=![]() )且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
)且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 甲由于看错了方程(1)中的a,得到方程组的解为
甲由于看错了方程(1)中的a,得到方程组的解为![]() , 乙由于看错了方程(2)中的b,得到方程组的解为
, 乙由于看错了方程(2)中的b,得到方程组的解为![]() , 若按正确的计算,求x+6y的值.
, 若按正确的计算,求x+6y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com