
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| DN |
| PN |
| t-1 | ||||
2-(-
|
| t-1 | ||
|
| 2 |
| t-1 |
| 2 |
| t-1 |
| DM |
| EM |
| DF |
| ED |
| PE |
| EA |
| 6 |
| 6 |
| PE |
| AE |
| 6 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
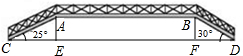 如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°
如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
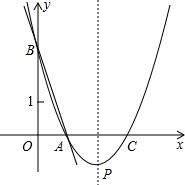 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:
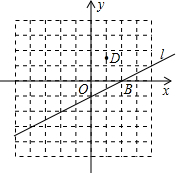 如图,已知直线l的解析式为y=
如图,已知直线l的解析式为y=| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com