Question

【题目】如图，等边△ABC 中，高线 AD=6，点P从点 A出发，沿着AD运动到点 D停止，以CP为边向左下方作等边△CPQ，连接BQ，DQ.

（1）请说明：△ACP ≌△BCQ；

（2）在点P的运动过程中，当△BDQ是等腰三角形时，求∠BDQ的度数；

Answer 1

【答案】（1）证明见解析；（2）∠BDQ=30°或75°或120°.

【解析】试题分析：（1）由等边三角形的性质得AC=BC，PC=QC，∠ACB=∠PCQ=60°，由边角边证得△ACP≌△BCQ；（2）由全等三角形的性质以及等边三角形的性质可得∠QBD=30°，由等腰三角形的性质，分情况求出∠BDQ.

试题解析：（1）∵△ABC和△PQC是等边三角形，

∴AC=BC，PC=QC，∠ACB=∠PCQ=60°，

又∵∠ACP=60°-∠BCP，∠BCQ=60°-∠BCP，

∴∠ACP=∠BCP

在△ACP和△BCQ中，

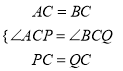
∴△ACP≌△BCQ（SAS）.

（2）由（1）知，△ACP ≌△BCQ，

∴∠QBD=∠PAC=30°，

当△BDQ 是等腰三角形时，

①若BQ=QD，如图1，则∠BDQ=30°；

②若BQ=BD，如图2，则∠BDQ=75°；

③若BD=DQ，如图3，则∠BDQ=120°.