
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1 个 |
分析 ①由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确.
②由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB,
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°-∠ABD;④由∠BAC+∠ABC=∠ACF,得出$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACF,再与∠BDC+∠DBC=$\frac{1}{2}$∠ACF相结合,得出$\frac{1}{2}$∠BAC=∠BDC,即∠BDC=$\frac{1}{2}$∠BAC.
解答 解:①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确.
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确.
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正确;
④∵∠BAC+∠ABC=∠ACF,
∴$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACF,
∵∠BDC+∠DBC=$\frac{1}{2}$∠ACF,
∴$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=∠BDC+∠DBC,
∵∠DBC=$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠BAC=∠BDC,即∠BDC=$\frac{1}{2}$∠BAC.
故④正确.
故选C.
点评 本题主要考查了三角形的内角和,平行线的判定和性质,三角形外角的性质等知识,解题的关键是正确找各角的关系.


科目:初中数学 来源: 题型:解答题
 星期天早晨,小明骑自行车从家里到植物园,途中到早餐店吃饭花了一段时间,然后继续骑行,直至到达植物园(假设在骑自行车过程中匀速行驶).
星期天早晨,小明骑自行车从家里到植物园,途中到早餐店吃饭花了一段时间,然后继续骑行,直至到达植物园(假设在骑自行车过程中匀速行驶).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小山岗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在与山脚C距离200m的D处,测得山顶A的仰角为26.6°,则小山岗的高AB=300米(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
如图,小山岗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在与山脚C距离200m的D处,测得山顶A的仰角为26.6°,则小山岗的高AB=300米(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
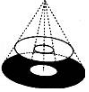 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com