

分析 (1)过点O作OH⊥BC于点H,连接OC,根据垂径定理求出CH的长,再根据勾股定理即可得出结论;
(2)根据(1)可得BH=CH,∠OHB=90°,故OH∥AB∥CD,再由平行线分线段成比例定理即可得出结论;
(3)①过点O作OM⊥CD交CD于点M,交FG于点N,根据AF⊥CD,DG⊥CD可得出AF∥ON∥DG.再由AO=DO可知FN=GN,根据垂径定理即可得出结论;
②作OP⊥BC交BC于点P,交AE于点Q,连接OC,OF,则OC=OF=5.由①知,FN=OQ=EM=$\frac{1}{2}$FG=3,OM=QE=$\frac{1}{2}$BC=4,设EF=x,则CM=CE+EM=7,QF=QE+EF=4+x,在Rt△OMC与Rt△OQF中根据勾股定理求出x的值,再由矩形的面积公式即可得出结论.
解答 (1)解:如图1,过点O作OH⊥BC于点H,连接OC,
∵圆O的半径为5,BC=6,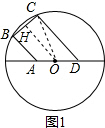
∴CH=$\frac{1}{2}$BC=3,
∴OH=$\sqrt{{OC}^{2}-{CH}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
(2)证明:∵由(1)得BH=CH,∠OHB=90°,
∴OH∥AB∥CD,
∴$\frac{BH}{CH}$=$\frac{AO}{DO}$=1,
∴OA=OD;
(3)①证明:如图2,过点O作OM⊥CD交CD于点M,交FG于点N,
∵AF⊥CD,DG⊥CD,
∴AF∥ON∥DG.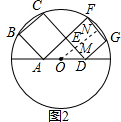
∵AO=DO,
∴FN=GN,
∴ON⊥FG.
∵AF∥ON,
∴AF⊥FG,
∴∠F=90°.
②解:如图3,作OP⊥BC交BC于点P,交AE于点Q,连接OC,OF,则OC=OF=5.
∵由①知,FN=OQ=EM=$\frac{1}{2}$FG=3,OM=QE=$\frac{1}{2}$BC=4,
∴设EF=x,则CM=CE+EM=7,QF=QE+EF=4+x,
在Rt△OMC与Rt△OQF中,
∵OC2=OM2+CM2=42+72=65,
OF2=OQ2+QF2=32+(4+x)2,
∴9+(4+x)2=65,
∴x=2$\sqrt{14}$-4,
∴S四边形EFGD=EF•FG=(2$\sqrt{14}$-4)×6=12$\sqrt{14}$-24.
点评 本题考查的是圆的综合题,涉及到垂径定理、勾股定理、矩形的面积公式等知识,在解答此类问题时要注意作出辅助线,构造出直角三角形求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
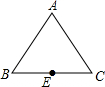 如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)
如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | ±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
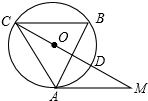 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
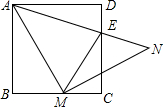 如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.
如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
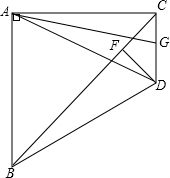 如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温 | 10℃ | 12℃ | 11℃ | 9℃ | 7℃ | 5℃ | 7℃ |
| 最低气温 | 2℃ | 1℃ | 0℃ | -1℃ | -4℃ | -5℃ | -5℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com