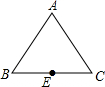Question

18．如图，是正三角形的人工湖，彤彤家住在湖顶点A处，她每天都要划船去湖对岸上学，学校位于BC中点E处，已知湖边长400$\sqrt{3}$米，彤彤划船的最快速度为30米/分，学校要求7：50到校，请你帮助彤彤算一算，她最晚几点从家里出发才不会迟到？（陆地时间忽略不计）

Answer 1

分析 连接AE，根据等边三角形的三线合一的性质得到AE⊥BC，从而得到直角三角形，利用勾股定理求得AE的长除以速度即可求得时间，从而确定答案．

解答 解：如图，连接AE，
∵△ABC为等边三角形，E为BC的中点，
∴AE⊥BC，
∵AB=BC=AC=400$\sqrt{3}$，
∴BE=EC=200$\sqrt{3}$，
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=600米，
∵彤彤划船的最快速度为30米/分，
∴彤彤划船的最少时间为600÷30=20分，
∵学校要求7：50到校，
∴她最晚7：30从家里出发才不会迟到．

点评 本题考查了等边三角形的性质及勾股定理的应用，解题的关键是从实际问题中整理出直角三角形，难度不大．