
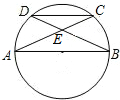
 如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.
如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°. 科目:初中数学 来源: 题型:解答题
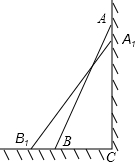 如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
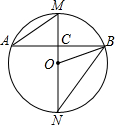 如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
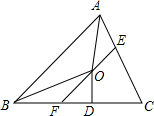 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
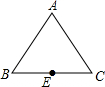 如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)
如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com