
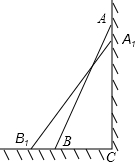
 如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度. 分析 在直角三角形ABC中,已知AB,AC,根据勾股定理即可求BC的长度,根据B1C=B1B+BC即可求得B1C的长度,在直角三角形A1B1C中,已知A1B1=AB,B1C,即可求得A1C的长度,根据AA1=AC-A1C即可求得A1A的长度.
解答  解:根据题意,在Rt△ABC中,AB=2.5,AC=2.4,
解:根据题意,在Rt△ABC中,AB=2.5,AC=2.4,
由勾股定理得:
BC=$\sqrt{2.{5}^{2}-2.{4}^{2}}$=0.7,
∵BB1=0.8,
∴B1C=B1B+BC=1.5.
∵在Rt△A1B1C中,A1B1=2.5,B1C=1.5,
∴A1C=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2,
∴A1A=2.4-2=0.4.
答:那么梯子顶端沿墙下滑的距离为0.4米.
点评 本题考查的是勾股定理的应用及勾股定理在直角三角形中的正确运用,本题中求B1C的长度是解题的关键.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化(m) | +0.25 | +0.80 | -0.40 | +0.03 | +0.28 | -0.36 | -0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com