
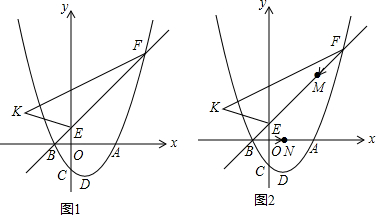
分析 (1)利用对称轴公式以及点$({2,-\frac{3}{2}})$代入,列出方程组解决.
(2)要求△KEF的面积只要知道EF以及边EF上的高,通过证明发现这个高就是线段BK,由此可以解决问题.
(3)求出点E′坐标,根据MN=NE′列出方程解决.
解答 解:(1)由题意:$\left\{\begin{array}{l}{-\frac{-1}{2a}=1}\\{4a-2+c=-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-\frac{3}{2}}\end{array}\right.$,所以抛物线解析式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,点C(0,-$\frac{3}{2}$).
(2)如图1中,FP⊥x轴,DH⊥OA垂足分别为P、H,连接BD、KB.
令y=0得$\frac{1}{2}$x2-x-$\frac{3}{2}$=0解得x=-1或3,所以B(-1,0),A(3,0),
设直线BE为:y=kx+b,
∵y=kx+b经过点B(-1,0),E(0,1)
∴$\left\{\begin{array}{l}{b=1}\\{-k+b=0}\end{array}\right.$,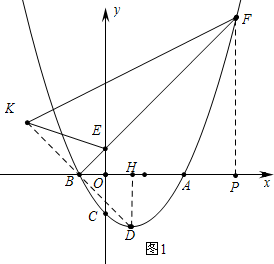
∴$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线BE为y=x+1,
由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.或\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$,
∴点F坐标(5,6),
∴PB=PF=6,∠FBP=45°,
∵抛物线顶点D(1,-2),
∴BH=DH=2,
∴∠HBD=∠HDB=45°,
∴∠DBF=90°,
∴DB⊥BE,
∵D、K关于直线BE对称,
∴K、B、D共线,
∴KB=BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵EF=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴S△EFK=$\frac{1}{2}$•EF•KB=$\frac{1}{2}$$•5\sqrt{2}•2\sqrt{2}$=10.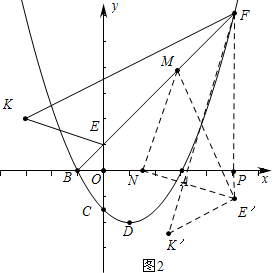 (3)存在.理由如下:
(3)存在.理由如下:
如图2中,由(1)可知∠BFP=∠FBP=45°,
∵EF=5$\sqrt{2}$,△FE′K′是由△FEK逆时针旋转45°得到,
∴点E′在直线FP上,
∴E′(5,5$\sqrt{2}$-6),
∵点N在ME′的垂直平分线上,
∴NM=NE,
∵点N坐标(t-1,0),点M坐标(5-t,6-t),
∴(t-1-5+t)2+(6-t)2=(5-t+1)2+(5$\sqrt{2}$-6)2,
∴t=$\frac{5\sqrt{2}}{2}$或6-$\frac{5\sqrt{2}}{2}$.
点评 本题考查二次函数、一次函数的有关性质、等腰三角形的性质、旋转不变性等知识,利用特殊三角形(等腰直角三角形)是解决本题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
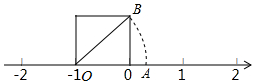 如图所示,认真观察,探讨下列问题:
如图所示,认真观察,探讨下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
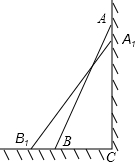 如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
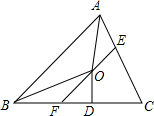 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com