
分析 先设直线的解析式为y=kx+b(k≠0),再把A(3,5)、B(-4,-9)代入求出k的值,进而得出直线AB的解析式,把点C(m,9)代入求出m的值即可.
解答 解:设直线的解析式为y=kx+b(k≠0),
∵A(3,5)、B(-4,-9),
∴$\left\{\begin{array}{l}{5=3k+b}\\{-9=-4k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为y=2x-1,
∵C(m,9)在直线上,
∴9=2m-1,解得m=5.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
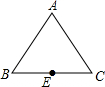 如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)
如图,是正三角形的人工湖,彤彤家住在湖顶点A处,她每天都要划船去湖对岸上学,学校位于BC中点E处,已知湖边长400$\sqrt{3}$米,彤彤划船的最快速度为30米/分,学校要求7:50到校,请你帮助彤彤算一算,她最晚几点从家里出发才不会迟到?(陆地时间忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
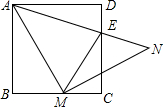 如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.
如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com