
 如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由. 分析 由两直线图象均过点A,可得出直线OA和直线l的表达式,设出D点坐标(m,n).以A,B,C,D为顶点的四边形是平行四边形分成两种情况,①以线段AB为对角线,此时利用平行四边形对角线互相平分的性质即可得出结论;②以线段AB为边,又要分CD在AB上或下方考虑,由平行四边形的性质,对比相等可得出结论.
解答 解:假设存在,设D点坐标为(m,n),直线OA解析式为y=kx.
∵点A(2,1)在直线OA上,
∴1=2k,解得:k=$\frac{1}{2}$.
即直线OA的解析式为y=$\frac{1}{2}$x.
∵D点在直线OA上,
∴D点坐标为(m,$\frac{1}{2}$m).
∵点A(2,1)在直线l上,
∴1=4+b,解得:b=-3.
使得以A,B,C,D为顶点的四边形是平行四边形分两种情况:
①以线段AB为对角线,如图1,令线段AB的中点为M.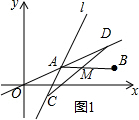
∵点A的坐标是(2,1),点B的坐标是(5,1),
∴点M的坐标是($\frac{7}{2}$,1).
∵四边形ACBD为平行四边形,点D坐标为(m,$\frac{1}{2}$m),
∴点C坐标为(7-m,2-$\frac{1}{2}$m).
又∵点C在直线l上,
∴有2-$\frac{1}{2}$m=2×(7-m)-3,解得:m=6.
此时D点坐标为(6,3).
②以线段AB为边,当C、D均在直线AB上方时,如图2.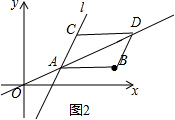
此时点C的坐标为(m-3,$\frac{1}{2}$m).
∵点C在直线l上,
∴有$\frac{1}{2}$m=2×(m-3)-3,解得:m=6.
此时D点的坐标为(6,3).
当C、D均在直线AB下方时,如图3.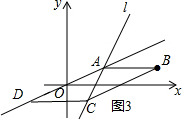
此时点C的坐标为(m+3,$\frac{1}{2}$m).
∵点C在直线l上,
∴有$\frac{1}{2}$m=2×(m+3)-3,解得:m=-2.
此时D点的坐标为(-2,-1).
综上可知:存在使得以A,B,C,D为顶点的四边形是平行四边形的D点,点D的坐标为(6,3)和(-2,-1).
点评 本题考查了一次函数综合应用中的由点在直线求直线表达式以及平行四边形的性质,解题的关键是依据平行四边形的性质①对角线互相平分;②对边相等来解决问题.本题难度不大,失分点是同学们往往忘记在考虑以线段AB为边时还存在两种情况,从而少的出一种结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一张面积为48cm2的正方形硬纸板的四周各剪去一个同样大小的面积为3cm2的小正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),那么这个长方体盒子的体积是多少?
如图,在一张面积为48cm2的正方形硬纸板的四周各剪去一个同样大小的面积为3cm2的小正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),那么这个长方体盒子的体积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
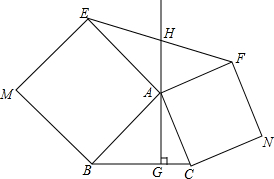 同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.
同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com