

分析 (1)要证AC•CD=PC•BC,只需证$\frac{CA}{CP}=\frac{CB}{CD}$,只需证△ACB∽△PCD;
(2)设AC=3x,则有BC=4x,AB=5x=10,从而可求出x,即可求出AC、BC,△ABC的面积,然后利用相似三角形的性质可得$\frac{{S}_{△ACB}}{{S}_{△PCD}}$=($\frac{AC}{PC}$)2,即可得到S△PCD=$\frac{2}{3}$PC2.要求△PCD面积的最大值,只需求出PC的最大值即可;
(3)连接OC,如图2.易证PM是⊙O的直径,即PM经过点O.由AQ=9,BQ=16,可求出AB、OA、OQ,根据勾股定理的逆定理可得∠CQO=90°,即可得到AB∥CD,根据平行线分线段成比例可得$\frac{CQ}{CP}=\frac{DB}{DP}$.根据垂径定理可得CQ=PQ=$\frac{1}{2}$PC,从而可得PC=2CQ=24,DB=$\frac{1}{2}$DP.由$\frac{CP}{CD}$=$\frac{CA}{CB}$=$\frac{3}{4}$可求出CD,根据勾股定理可求出PD,从而可求出DB,在Rt△PCM中运用勾股定理可求出CM.由CM∥OB可得△CNM∽△BNO,根据相似三角形的性质可求出MN.
解答 解:(1)∵AB是⊙O的直径,∠PCD=90°,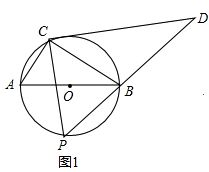
∴∠ACB=∠PCD=90°.
∵∠CAB=∠CPD,
∴△ACB∽△PCD,
∴$\frac{CA}{CP}=\frac{CB}{CD}$,
∴AC•CD=PC•BC;
(2)设AC=3x,
∵$\frac{AC}{BC}=\frac{3}{4}$,∴BC=4x,
∴AB=5x=10,
∴x=2,
∴AC=6,BC=8,
∴S△ABC=$\frac{1}{2}$AC•BC=24.
∵△ACB∽△PCD,
∴$\frac{{S}_{△ACB}}{{S}_{△PCD}}$=($\frac{AC}{PC}$)2,
∴$\frac{24}{{S}_{△PCD}}$=$\frac{36}{P{C}^{2}}$,
∴S△PCD=$\frac{2}{3}$PC2.
∴当PC最大即PC为⊙O直径时,S△PCD最大,
此时PC=10,S△PCD=$\frac{2}{3}$×100=$\frac{200}{3}$;
(3)连接OC,如图2.
∵∠PCD=90°,∴PM是⊙O的直径,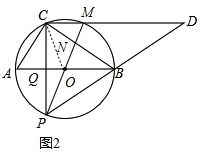
∴PM经过点O.
∵AQ=9,BQ=16,
∴AB=25,OA=$\frac{25}{2}$,OQ=$\frac{25}{2}$-9=$\frac{7}{2}$.
∵CQ=12,OC=$\frac{25}{2}$,
∴OQ2+CQ2=($\frac{7}{2}$)2+122=$\frac{625}{4}$=OC2,
∴∠CQO=90°,
∴∠CQB+PCD=180°,
∴AB∥CD,
∴$\frac{CQ}{CP}=\frac{DB}{DP}$.
∵∠CQO=90°即AB⊥CP,
∴CQ=PQ=$\frac{1}{2}$PC.
∴PC=2CQ=24,DB=$\frac{1}{2}$DP.
∵$\frac{CP}{CD}$=$\frac{CA}{CB}$=$\frac{3}{4}$,
∴CD=32,
∴PD=$\sqrt{P{C}^{2}+C{D}^{2}}$=40,DB=$\frac{1}{2}$DP=20.
在Rt△PCM中,
∵PC=24,PM=AB=25,
∴CM=$\sqrt{P{M}^{2}-P{C}^{2}}$=7.
∵CM∥OB,
∴△CNM∽△BNO,
∴$\frac{CM}{BO}$=$\frac{MN}{NO}$,
∴$\frac{7}{\frac{25}{2}}$=$\frac{MN}{\frac{25}{2}-MN}$,
解得MN=$\frac{175}{39}$.
点评 本题主要考查了相似三角形的判定与性质、圆周角定理、勾股定理及其逆定理、平行线的判定与性质、平行线分线段成比例、垂径定理等知识,具有一定的综合性,运用相似三角形的面积比等于相似比的平方是解决第(2)小题的关键,证到∠CQO=90°进而得到AB∥CD是解决第(3)小题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+2y=1}\\{3y-z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=5}\\{x-y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=2}\\{xy=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=3x-2}\\{\frac{2}{x}-1=0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com